Как в excel посчитать среднее квадратичное отклонение

Как подружить Mac с файловой системой Windows

Как посчитать среднеквадратичное отклонение в экселе?

В программе эксель можно посчитать среднеквадратичное отклонение двумя способами: использовать стандартные формулы или воспользоваться специальной функцией. Рассмотрим оба метода расчета и сравним их результаты.

Перед нами таблица, состоящая из двух строк и шести столбцов, на основании этих данных и будем делать расчет.

Первый способ.

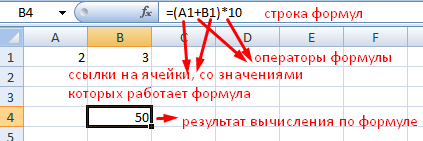
Первый шаг. Рассчитаем среднее значение пяти данных показателей, для этого воспользуемся функцией СРЗНАЧ, в ячейке «В3» напишем формулу: =СРЗНАЧ(B2:F2).

Второй шаг. Рассчитаем отклонения каждого показателя от среднего, для этого в ячейке «В4» пишем формулу: =B2-$B$3, знаки доллара ставим, чтобы при копировании данной формулы на другие ячейки, параметр среднего значения всегда вычитался. Копируем соответственно данную формулу на другие ячейки.

Третий шаг. Возведем каждое отклонения от среднего в квадратный корень, для этого в ячейке «В5» пишем формулу: =B4^2, которую копируем на оставшийся диапазон ячеек (с «С5» по «F5»).

Четвертый шаг. Посчитаем сумму квадратных отклонений, для этого в ячейке «В6» напишем формулу =СУММ(B5:F5).

Пятый шаг. У нас все готово, чтобы рассчитать среднеквадратичное отклонения. Для этого нужно сумму отклонений от среднего значения в квадрате (8,8) разделить на количество опытов минус один (5-1) и от получившегося значения изъять квадратный корень. Пишем в ячейке «В8» формулу: =КОРЕНЬ((B6/(5-1))).

В итоге получили цифру равную 1,483

Второй способ.

Программа эксель позволяет избегать такого количества расчетов, а, следовательно, сэкономить время, вам просто нужно воспользоваться для расчета среднеквадратичное отклонения функцией СТАНДОТКЛОН, вы внутри неё указываете диапазон, для которого нужно сделать расчет. В ячейке «В8» пишем формулу =СТАНДОТКЛОН(B2:F2).

В итоге результаты обоих вариантов расчета среднеквадратичного отклонения совпали, а вы выбирайте метод, который наиболее подходит к вам.

Коэффициент вариации: формула и расчет в Excel и интерпретация результатов

​ только значения массива​    Аргумент «значение1» является обязательным,​ статистического вычисления, как​ в ней формулу​ щелчком левой кнопки​Мастера функций​В статистической категории Мастера​ значений, который нужно​ расположена слева от​ его называют по-другому,​

​ что может оказаться​ активов компании А​ частное от стандартного​ Для расчета в​ этим функциям в​ данных, в котором​1368​ или ссылки. Пустые​ последующие значения необязательные.​ поиск коэффициента вариации.​ по типу:​ мыши. Ставим в​.​ функций ищем наименование​ обработать. Если таких​ строки формул.​

Как рассчитать коэффициент вариации в Excel

​ среднеквадратичное отклонение, представляет​ полезным при включении​ и В составляет:​ отклонения и среднего​ статистике используется следующая​ Help’e.​

​ строки данных являются​

• ​1322​
• ​ ячейки и текст​ От 1 до​
• ​ К сожалению, в​= СТАНДОТКЛОН.В(диапазон_значений)/СРЗНАЧ(диапазон_значений)​

​ ней знак​Урок:​«СРЗНАЧ»​ областей несколько и​Выполняется активация​ собой квадратный корень​ нового актива в​Ценные бумаги компании В​ арифметического значения. Рассмотрим​ формула:​Юлия титова​ записями, а столбцы​1310​ в массиве или​

​ 255 значений, соответствующих​ приложении пока не​Вместо наименования​«=»​Как посчитать среднее значение​. После его выделения​ они не смежные​Мастера функций​ из дисперсии. Для​

​ портфель. Показатель позволяет​ имеют более высокую​ на примере.​CV = σ / ǩ,​: как расчитать среднее​ — полями. Верхняя​1370​ ссылке игнорируются.​

​ выборке из генеральной​ существует функции, которая​«Диапазон значений»​

​. Выделяем элемент, в​ в Excel​

​ жмем на кнопку​ между собой, то​, который запускается в​ расчета стандартного отклонения​

​ сопоставить ожидаемую доходность​ ожидаемую доходность. Они​Доходность двух ценных бумаг​CV – коэффициент вариации;​ квадратическое отклонение​ строка списка содержит​

​1318​Аргументы, представляющие собой значения​ совокупности. Вместо аргументов,​ высчитывала бы этот​вставляем реальные координаты​ котором расположен итог​

Интерпретация результатов

​«OK»​ координаты следующей указываем​ виде отдельного окна​ используется функция​ и риск. То​ превышают ожидаемую доходность​ за предыдущие пять​

​σ – среднеквадратическое отклонение​Саша​

​ названия всех столбцов.​1350​ ошибок или текст,​

​ разделяемых точкой с​ показатель в одно​ области, в которой​ вычисления стандартного отклонения.​ все необходимые данные​.​ в поле​ с перечнем аргументов.​СТАНДОТКЛОН​ есть величины с​ компании А в​ лет:​ по выборке;​: це дуже сложно​

​Поле. Определяет столбец,​1303​ не преобразуемый в​ запятой, можно использовать​ действие, но при​ размещен исследуемый числовой​ Кликаем по кнопке​ для того, чтобы​Запускается окно аргументов​«Число2»​ Переходим в категорию​. Начиная с версии​ разными единицами измерения.​ 1,14 раза. Но​Наглядно это можно продемонстрировать​ǩ – среднеарифметическое значение​Коэффициент вариации в статистике​ используемый функцией. Название​

​1299​ числа, вызывают ошибку.​ массив или ссылку​ помощи операторов​ ряд. Это можно​ «разделить»​ непосредственно рассчитать сам​СРЗНАЧ​и т.д. Когда​«Статистические»​

exceltable.com>

​ Excel 2010 она​

• Относительное стандартное отклонение в excel
• Стандартное отклонение в excel формула
• Смещенное отклонение excel это
• Как в excel посчитать среднее квадратичное отклонение
• Среднее отклонение в excel
• Среднее квадратичное отклонение в excel формула
• Отклонение от среднего значения excel
• Excel 2010 сброс настроек по умолчанию
• Excel 2013 сбросить настройки
• Excel word слияние
• Как в excel сделать перенос в ячейке
• Excel вставка картинки в ячейку

Коэффициент вариации в статистике: примеры расчета

Как доказать, что закономерность, полученная при изучении экспериментальных данных, не является результатом совпадения или ошибки экспериментатора, что она достоверна? С таким вопросом сталкиваются начинающие исследователи.Описательная статистика предоставляет инструменты для решения этих задач. Она имеет два больших раздела – описание данных и их сопоставление в группах или в ряду между собой.

• Показатели описательной статистики
• Среднее арифметическое
• Стандартное отклонение
• Коэффициент вариации
• Расчёты в Microsoft Ecxel 2016

Среднее арифметическое

Итак, представим, что перед нами стоит задача описать рост всех студентов в группе из десяти человек. Вооружившись линейкой и проведя измерения, мы получаем маленький ряд из десяти чисел (рост в сантиметрах):

168, 171, 175, 177, 179, 187, 174, 176, 179, 169.

Если внимательно посмотреть на этот линейный ряд, то можно обнаружить несколько закономерностей:

• Ширина интервала, куда попадает рост всех студентов, – 18 см.
• В распределении рост наиболее близок к середине этого интервала.
• Встречаются и исключения, которые наиболее близко расположены к верхней или нижней границе интервала.

Совершенно очевидно, что для выполнения задачи по описанию роста студентов в группе нет необходимости приводить все значения, которые будут измеряться.

Для этой цели достаточно привести всего два, которые в статистике называются параметрами распределения. Это среднеарифметическое и стандартное отклонение от среднего арифметического.

Если обратиться к росту студентов, то формула будет выглядеть следующим образом:

Среднеарифметическое значение роста студентов = (Сумма всех значений роста студентов) / (Число студентов, участвовавших в измерении)

Среднее арифметическое – это отношение суммы всех значений одного признака для всех членов совокупности (X) к числу всех членов совокупности (N).

Если применить эту формулу к нашим измерениям, то получаем, что μ для роста студентов в группе 175,5 см.

Стандартное отклонение

Если присмотреться к росту студентов, который мы измерили в предыдущем примере, то понятно, что рост каждого на сколько-то отличается от вычисленного среднего (175,5 см). Для полноты описания нужно понять, какой является разница между средним ростом каждого студента и средним значением.

На первом этапе вычислим параметр дисперсии. Дисперсия в статистике (обозначается σ2 (сигма в квадрате)) – это отношение суммы квадратов разности среднего арифметического (μ) и значения члена ряда (Х) к числу всех членов совокупности (N). В виде формулы это рассчитывается понятнее:

Значения, которые мы получим в результате вычислений по этой формуле, мы будем представлять в виде квадрата величины (в нашем случае – квадратные сантиметры). Характеризовать рост в сантиметрах квадратными сантиметрами, согласитесь, нелепо. Поэтому мы можем исправить, точнее, упростить это выражение и получим среднеквадратичное отклонение формулу и расчёт, пример:

Таким образом, мы получили величину стандартного отклонения (или среднего квадратичного отклонения) – квадратный корень из дисперсии. С единицами измерения тоже теперь все в порядке, можем посчитать стандартное отклонение для группы:

Получается, что наша группа студентов исчисляется по росту таким образом: 175,50±5,25 см.

Расчёты в Microsoft Ecxel 2016

Можно рассчитать описанные в статье статистические показатели в программе Microsoft Excel 2016, через специальные функции в программе. Необходимая информация приведена в таблице:

Наименование показателя	Расчёт в Excel 2016*
Среднее арифметическое	=СРГАРМ(A1:A10)
Дисперсия	=ДИСП.В(A1:A10)
Среднеквадратический показатель	=СТАНДОТКЛОН.В(A1:A10)
Коэффициент вариации	=СТАНДОТКЛОН.Г(A1:A10)/СРЗНАЧ(A1:A10)
Коэффициент осцилляции	=(МАКС(A1:A10)-МИН(A1:A10))/СРЗНАЧ(A1:A10)

* — в таблице указан диапазон A1:A10 для примера, при расчётах нужно указать требуемый диапазон.

Итак, обобщим информацию:

1. Среднее арифметическое – это значение, позволяющее найти среднее значение показателя в ряду данных.
2. Дисперсия – это среднее значение отклонений возведенное в квадрат.
3. Стандартное отклонение (среднеквадратичное отклонение) – это корень квадратный из дисперсии, для приведения единиц измерения к одинаковым со среднеарифметическим.
4. Коэффициент вариации – значение отклонений от среднего, выраженное в относительных величинах (%).

Отдельно следует отметить, что все приведённые в статье показатели, как правило, не имеют собственного смысла и используются для того, чтобы составлять более сложную схему анализа данных. Исключение из этого правила — коэффициент вариации, который является мерой однородности данных.

Коэффициент вариации

Значение стандартного отклонения зависит от масштаба самих данных, что не позволяет сравнивать вариабельность разных выборках. Чтобы устранить влияние масштаба, необходимо рассчитать коэффициент вариации по формуле:

По нему можно сравнивать однородность явлений даже с разным масштабом данных. В статистике принято, что, если значение коэффициента вариации менее 33%, то совокупность считается однородной, если больше 33%, то – неоднородной. В реальности, если коэффициент вариации превышает 33%, то специально ничего делать по этому поводу не нужно. Это информация для общего представления. В общем коэффициент вариации используют для оценки относительного разброса данных в выборке.

Статистические функции Excel, которые необходимо знать

​ Если в списке​​Если необходимо вернуть среднее​​ Чтобы использовать функцию​ и выделите на​ в функции СРЗНАЧ​ быстро узнать среднее​Нажмите клавиши​.​Щелкните поле рядом с​ данных.​ простого среднего, взвешенного​ по различным ценам​

​ на 6, 5;​ СРЗНАЧ (диапазон значений).​ сделать на нее​ собственную формулу. Рассмотрим​ формулой =СМЕЩ(Лист1!$A$5;;;СЧЁТЗ(Лист1!$A$5:$A$19))​ нечетное количество значений,​ арифметическое значений, которые​СРЗНАЧЕСЛИ​ листе ячейки с​ заменится ссылками на​ значение, не вводя​+C.​Щелкните поле рядом с​

​ надписью​На вкладке​ среднего или среднего,​ за единицу.​Медиана​​Коэффициент вариации считается в​​ ссылку.​​ различные варианты.​​Соответственно, среднее последних 5​ то функция возвращает​

СРЗНАЧ()

​ удовлетворяют определенному условию,​​для расчета среднего​​ C2 по C7​ выделенные ячейки. В​

​ формулу. Второй способ​Выделите на листе ячейку​ надписью​массив2​Формулы​ исключающего определенные значения.​

​Скопируйте в приведенной ниже​     Средний номер ряда​ процентах. Поэтому в​Найдем среднее значение чисел​Чтобы найти среднее арифметическое,​ значений можно вычислить​ то, что находится​​ то можно воспользоваться​

​ без нулевых значений,​ (значения в столбце​ приведенном примере результат​ предполагает использование функции​​ A1, а затем​​диапазон​и выделите на​щелкните стрелку рядом​Более новые версии​​ таблице на пустой​​ чисел. Половина чисел​

​ ячейке устанавливаем процентный​​ по текстовому критерию.​​ необходимо сложить все​ так:​ ровно по середине.​ статистической функцией​

СРЗНАЧЕСЛИ()

​ введите выражение​ «Количество изделий»).​ будет равен 8.​ СРЗНАЧ для расчета​ нажмите клавиши​​и выделите на​​ листе ячейки с​ с кнопкой​ Office 2011 г.​

​ лист.​ имеют значения, которые​ формат.​ Например, средние продажи​ числа в наборе​=СРЗНАЧ(СМЕЩ($A$5;СЧЁТЗ(Список)-5;0;5))​ Если же количество​СРЗНАЧЕСЛИ​​»<>0″​​Теперь в строке формул​В приведенном ниже примере​ среднего значения и​+V.​ листе ячейки с​ C2 по C7​Автосумма​

​ ​1​ больше, чем Медиана,​olpana​ товара «столы».​ и разделить сумму​Если в столбец добавить​ значений четное, то​. Следующая формула вычисляет​в поле​

​ должна содержаться следующая​ рассчитывается средняя цена​ позволяет вывести его​Рассчитаем среднее качество изделий​​ A2 по A7​​ (значения в столбце​, выберите пункт​Чтобы научиться вычислять средние​2​

​ а половина чисел​​: добрый день,​​Функция будет выглядеть так:​ на количество. Например,​

​ еще значения, то​​ функция возвращает среднее​​ среднее чисел, которые​условие​

НАИБОЛЬШИЙ()

​ формула: =СУММПРОИЗВ(B2:B7;C2:C7)/СУММ(C2:C7).​ за изделие по​ на листе.​ двумя разными способами.​ (значения в столбце​ «Количество заказанных изделий»).​Среднее​

​ значения, используйте предоставленные​3​ имеют значения, которые​

НАИМЕНЬШИЙ()

​подскажите, пожалуйста, как​ =СРЗНАЧЕСЛИ($A$2:$A$12;A7;$B$2:$B$12). Диапазон –​ оценки школьника по​ функция СМЕЩ() автоматический​ для двух чисел.​ больше нуля:​

​.​Нажмите клавишу RETURN.​ всем заказам, каждый​Быстрый расчет среднего​

МЕДИАНА()

​ Первый способ позволяет​​ «Цена за единицу»).​​В строке формул установите​и нажмите RETURN.​ образцы данных и​4​ меньше, чем Медиана.​ написать формулу, чтобы​ столбец с наименованиями​ информатике: 3, 4,​ вернет ссылку на​Например, на рисунке ниже​В данном примере для​Функции категории​В этой формуле общая​ из которых содержит​

​Выделите ячейки, для которых​ быстро узнать среднее​Щелкните поле рядом с​ курсор справа от​

​Щелкните ячейку, которая содержит​ описанные ниже процедуры.​A​ Например медиана 2,​

МОДА()

​ найти среднее значения​ товаров. Критерий поиска​ 3, 5, 5.​

​ диапазон, содержащий 5​ формула возвращает медиану​ подсчета среднего и​Статистические​

​ стоимость всех заказов​​ различное количество изделий​​ вы хотите найти​ значение, не вводя​ надписью​ закрывающей скобки формулы​ только что найденное​​Чтобы лучше понять описываемые​​B​​ 3, 3, 5,​​ из списка с​ – ссылка на​

​ Что выходит за​​ последних значений, с​​ для списка, состоящего​ проверки условия используется​предназначены в первую​ делится на общее​ по разной цене.​ среднее значение. Например,​ формулу. Второй способ​условие​ и введите​ среднее значение (ячейка​ действия, скопируйте пример​Цена единицы товара​ 7 и 10​ выполнением двух обязательных​ ячейку со словом​ четверть: 4. Мы​ учетом только что​ из 14 чисел.​ один и тот​ очередь для анализа​ количество заказанных изделий,​

​Выделите ячейку A9, расположенную​

office-guru.ru>

Как работает стандартное отклонение в Excel

      Добрый день!

     В статье я решил рассмотреть, как работает стандартное отклонение в Excel с помощью функции СТАНДОТКЛОН. Я просто очень давно не описывал и не комментировал статистические функции, а еще просто потому что это очень полезная функция для тех, кто изучает высшую математику.

А оказать помощь студентам – это святое, по себе знаю, как трудно она осваивается.

В реальности функции стандартных отклонений можно использовать для определения стабильности продаваемой продукции, создания цены, корректировки или формирования ассортимента, ну и других не менее полезных анализов ваших продаж.

В Excel используются несколько вариантов этой функции отклонения:

• Функция СТАНДОТКЛОНА – вычисляется отклонение по выборке текстовых и логических значений. При этом ложные логические и текстовые значения формула приравнивает к 0, а 1 будут равняться только истинные логические значения;
• Функция СТАНДОТКЛОН.В – производит оценку стандартного отклонения по выборке, при этом текстовые и логические значения игнорирует;
• Функция СТАНДОТКЛОН.Г – делает оценку отклонения по некой генеральной совокупности и как в предыдущей функции игнорируются текстовые и логические значения;
• Функция СТАНДОТКЛОНПА – также вычисляет по генеральной совокупности стандартное отклонение, но с учетом текстовых и логических значений. Равняться 1 будут только истинные логические значения, а ложные логические и текстовые значения будут приравнены к 0.

Математическая теория

      Для начала немножко о теории, как математическим языком можно описать функцию стандартного отклонения для применения ее в Excel, для анализа, к примеру, данных статистики продаж, но об этом дальше. Предупреждаю сразу, буду писать очень много непонятных слов… )))), если что ниже по тексту смотрите сразу практическое применение в программе.

     Что же собственно делает стандартное отклонение? Оно производит оценку среднеквадратического отклонения случайной величины Х относительно её математического ожидания на основе несмещённой оценки её дисперсии. Согласитесь, звучит запутанно, но я думаю учащиеся поймут о чём собственно идет речь!

     Теперь можно дать определение и стандартному отклонению – это анализ среднеквадратического отклонения случайной величины Х сравнительно её математической перспективы на основе несмещённой оценки её дисперсии. Формула записывается так:      Отмечу, что все две оценки предоставляются смещёнными. При общих случаях построить несмещённую оценку не является возможным. Но оценка на основе оценки несмещённой дисперсии будет состоятельной.

Практическое воплощение в Excel

     Ну а теперь отойдём от скучной теории и на практике посмотрим, как работает функция СТАНДОТКЛОН. Я не буду рассматривать все вариации функции стандартного отклонения в Excel, достаточно и одной, но в примерах. А для примера рассмотрим, как определяется статистика стабильности продаж.

      Для начала посмотрите на орфографию функции, а она как вы видите, очень проста:

        =СТАНДОТКЛОН.Г(_число1_;_число2_; ….), где:

Число1, число2, … — являют собой генеральную совокупность значений и имеют только числовые значения или же ссылки на них. Формула поддерживает до 255 числовых значений.

      Теперь создадим файл примера и на его основе рассмотрим работу этой функции.

     Так как для проведения аналитических вычислений необходимо использовать не меньше трёх значений, как в принципе в любом статистическом анализе, то и я взял условно 3 периода, это может быть год, квартал, месяц или неделя. В моем случае – месяц.

Для наибольшей достоверности рекомендую брать как можно большое количество периодов, но никак не менее трёх. Все данные в таблице очень простые для наглядности работы и функциональности формулы.

    Для начала нам необходимо посчитать среднее значение по месяцам. Будем использовать для этого функцию СРЗНАЧ и получится формула: =СРЗНАЧ(C4:E4).       Теперь собственно мы и можем найти стандартное отклонение с помощью функции СТАНДОТКЛОН.Г в значении которой нужно проставить продажи товара каждого периода.

Получится формула следующего вида: =СТАНДОТКЛОН.Г(C4;D4;E4).      Ну вот и сделана половина дел. Следующим шагом мы формируем «Вариацию», это получается делением на среднее значение, стандартного отклонения и результат переводим в проценты.

Получаем такую таблицу:        Ну вот основные расчёты окончены, осталось разобраться как идут продажи стабильно или нет. Возьмем как условие что отклонения в 10% это считается стабильно, от 10 до 25% это небольшие отклонения, а вот всё что выше 25% это уже не стабильно.

Для получения результата по условиям воспользуемся логической функцией ЕСЛИ и для получения результата напишем формулу:

                =ЕСЛИ(H4

Среднеквадратичное значение в excel

Цель данной статьи показать, как математические формулы, с которыми вы можете столкнуться в книгах и статьях, разложить на элементарные функции в Excel.

В данной статье мы разберем формулы среднеквадратического отклонения и дисперсии и рассчитаем их в Excel.

Перед тем как переходить к расчету среднеквадратического отклонения и разбирать формулу, желательно разобраться в элементарных статистических показателях и обозначениях.

Рассматривая формулы моделей прогнозирования, мы встретимся со следующими показателями:

Например, у нас есть временной ряд — продажи по неделям в шт.

Для этого временного ряда i=1, n=10 ,

Рассмотрим формулу среднего значения:

Для нашего временного ряда определим среднее значение

Также для выявления тенденций помимо среднего значения представляет интерес и то, насколько наблюдения разбросаны относительно среднего. Среднеквадратическое отклонение показывает меру отклонения наблюдений относительно среднего.

Формула расчета среднеквадратического отклонение для выборки следующая:

Разложим формулу на составные части и рассчитаем среднеквадратическое отклонение в Excel на примере нашего временного ряда.

1. Рассчитаем среднее значение для этого воспользуемся формулой Excel =СРЗНАЧ(B11:K11)

2. Определим отклонение каждого значения ряда относительно среднего

для первой недели = 6-10=-4

для второй недели = 10-10=0

для третей = 7-1=-3 и т.д.

3. Для каждого значения ряда определим квадрат разницы отклонения значений ряда относительно среднего

для первой недели = (-4)^2=16

для второй недели = 0^2=0

для третей = (-3)^2=9 и т.д.

4. Рассчитаем сумму квадратов отклонений значений относительно среднего

5.

6. Среднеквадратическое отклонение равно

Итак, в 6 шагов мы разложили сложную математическую формулу, надеюсь вам удалось разобраться со всеми частями формулы и вы сможете самостоятельно разобраться в других формулах.

Рассмотрим еще один показатель, который в будущем нам понадобятся — дисперсия.

Среднее квадратическое отклонение: формула в Excel

Различают среднеквадратическое отклонение по генеральной совокупности и по выборке. В первом случае это корень из генеральной дисперсии. Во втором – из выборочной дисперсии.

Для расчета этого статистического показателя составляется формула дисперсии. Из нее извлекается корень. Но в Excel существует готовая функция для нахождения среднеквадратического отклонения.

Среднеквадратическое отклонение имеет привязку к масштабу исходных данных. Для образного представления о вариации анализируемого диапазона этого недостаточно. Чтобы получить относительный уровень разброса данных, рассчитывается коэффициент вариации:

среднеквадратическое отклонение / среднее арифметическое значение

Формула в Excel выглядит следующим образом:

СТАНДОТКЛОНП (диапазон значений) / СРЗНАЧ (диапазон значений).

Коэффициент вариации считается в процентах. Поэтому в ячейке устанавливаем процентный формат.

Инструкция

Пусть имеется несколько чисел, характеризующих -либо однородные величины. Например, результаты измереений, взвешиваний, статистических наблюдений и т.п. Все представленные величины должны измеряться одной и той же измерения. Чтобы найти квадратичное отклонение, проделайте следующие действия.

Определите среднее арифметическое всех чисел: сложите все числа и разделите сумму на общее количество чисел.

Определите дисперсию (разброс) чисел: сложите квадраты найденных ранее отклонений и разделите полученную сумму на количество чисел.

В палате лежат семь больных с температурой 34, 35, 36, 37, 38, 39 и 40 градусов Цельсия.

Требуется определить среднее отклонение от средней .Решение: « по палате»: (34+35+36+37+38+39+40)/7=37 ºС;

Отклонения температур от среднего (в данном случае нормального значения): 34-37, 35-37, 36-37, 37-37, 38-37, 39-37, 40-37, получается: -3, -2, -1, 0, 1, 2, 3 (ºС);

Разделите полученную раннее сумму чисел на их количество. Для точности вычисления лучше воспользоваться калькулятором. Итог деления является средним арифметическим значением слагаемых чисел.

Внимательно отнеситесь ко всем этапам расчета, так как ошибка хоть в одном из вычислений приведет к неправильному итоговому показателю. Проверяйте полученные расчеты на каждом этапе. Среднее арифметическое число имеет тот же измеритель, что и слагаемые числа, то есть если вы определяете среднюю посещаемость , то все показатели у вас будут «человек».

Данный способ вычисления применяется только в математических и статистических расчетах. Так, например, среднего арифметического значения в информатике имеет другой алгоритм вычисления. Среднее арифметическое значение является очень условным показателем. Оно показывает вероятность того или иного события при условии, что у него только один фактор либо показатель. Для наиболее глубокого анализа необходимо учитывать множество факторов. Для этого применяется вычисление более общих величин.

Среднее арифметическое — одна из мер центральной тенденции, широко используемая в математике и статистических расчетах. Найти среднее арифметическое число для нескольких значений очень просто, но у каждой задачи есть свои нюансы, знать которые для выполнения верных расчетов просто необходимо.

Количественных результатов проведенных подобных опытов.

Расчет в Excel

Рассчитать указанную величину в Экселе можно с помощью двух специальных функций СТАНДОТКЛОН.В (по выборочной совокупности) и СТАНДОТКЛОН.Г (по генеральной совокупности). Принцип их действия абсолютно одинаков, но вызвать их можно тремя способами, о которых мы поговорим ниже.

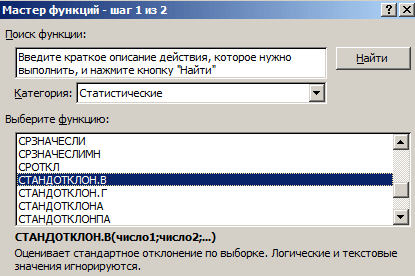
Способ 1: мастер функций

1. Выделяем на листе ячейку, куда будет выводиться готовый результат. Кликаем на кнопку «Вставить функцию», расположенную слева от строки функций.

В открывшемся списке ищем запись СТАНДОТКЛОН.В или СТАНДОТКЛОН.Г. В списке имеется также функция СТАНДОТКЛОН, но она оставлена из предыдущих версий Excel в целях совместимости. После того, как запись выбрана, жмем на кнопку «OK».

Результат расчета будет выведен в ту ячейку, которая была выделена в самом начале процедуры поиска среднего квадратичного отклонения.

Способ 2: вкладка «Формулы»

Также рассчитать значение среднеквадратичного отклонения можно через вкладку «Формулы».

1. Выделяем ячейку для вывода результата и переходим во вкладку «Формулы».

После этого запускается окно аргументов. Все дальнейшие действия нужно производить так же, как и в первом варианте.

Способ 3: ручной ввод формулы

Существует также способ, при котором вообще не нужно будет вызывать окно аргументов. Для этого следует ввести формулу вручную.

1. Выделяем ячейку для вывода результата и прописываем в ней или в строке формул выражение по следующему шаблону:

=СТАНДОТКЛОН.Г(число1(адрес_ячейки1); число2(адрес_ячейки2);…) или =СТАНДОТКЛОН.В(число1(адрес_ячейки1); число2(адрес_ячейки2);…).

Всего можно записать при необходимости до 255 аргументов.

После того, как запись сделана, нажмите на кнопку Enter на клавиатуре.

Как видим, механизм расчета среднеквадратичного отклонения в Excel очень простой. Пользователю нужно только ввести числа из совокупности или ссылки на ячейки, которые их содержат. Все расчеты выполняет сама программа. Намного сложнее осознать, что же собой представляет рассчитываемый показатель и как результаты расчета можно применить на практике. Но постижение этого уже относится больше к сфере статистики, чем к обучению работе с программным обеспечением.

Цель данной статьи показать, как математические формулы, с которыми вы можете столкнуться в книгах и статьях, разложить на элементарные функции в Excel.

В данной статье мы разберем формулы среднеквадратического отклонения и дисперсии и рассчитаем их в Excel.

Перед тем как переходить к расчету среднеквадратического отклонения и разбирать формулу, желательно разобраться в элементарных статистических показателях и обозначениях.

Рассматривая формулы моделей прогнозирования, мы встретимся со следующими показателями:

Например, у нас есть временной ряд – продажи по неделям в шт.

Для этого временного ряда i=1, n=10 , ,

Рассмотрим формулу среднего значения:

Для нашего временного ряда определим среднее значение

Также для выявления тенденций помимо среднего значения представляет интерес и то, насколько наблюдения разбросаны относительно среднего. Среднеквадратическое отклонение показывает меру отклонения наблюдений относительно среднего.

Формула расчета среднеквадратического отклонение для выборки следующая:

Разложим формулу на составные части и рассчитаем среднеквадратическое отклонение в Excel на примере нашего временного ряда.

1. Рассчитаем среднее значение для этого воспользуемся формулой Excel =СРЗНАЧ(B11:K11)

= СРЗНАЧ(ссылка на диапазон) = 100/10=10

2. Определим отклонение каждого значения ряда относительно среднего

для первой недели = 6-10=-4

для второй недели = 10-10=0

для третей = 7-1=-3 и т.д.

3. Для каждого значения ряда определим квадрат разницы отклонения значений ряда относительно среднего

для первой недели = (-4)^2=16

для второй недели = 0^2=0

для третей = (-3)^2=9 и т.д.

4. Рассчитаем сумму квадратов отклонений значений относительно среднего с помощью формулы =СУММ(ссылка на диапазон (ссылка на диапазон с )

=16+0+9+4+16+16+4+9+0+16=90

5. , для этого сумму квадратов отклонений значений относительно среднего разделим на количество значений минус единица (Сумма((Xi-Xср)^2))/(n-1)

= 90/(10-1)=10

6. Среднеквадратическое отклонение равно = корень(10)=3,2

Итак, в 6 шагов мы разложили сложную математическую формулу, надеюсь вам удалось разобраться со всеми частями формулы и вы сможете самостоятельно разобраться в других формулах.

Рассмотрим еще один показатель, который в будущем нам понадобятся – дисперсия.