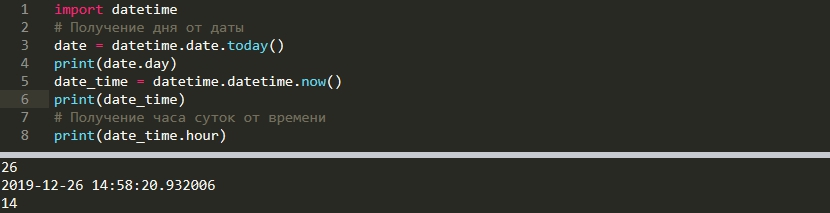
Модуль math в python

Веб-разработка

Python это популярный язык для веб-разработки.
Все пакеты Python, перечисленные в этом
разделе, делают жизнь веб-разработчика
гораздо проще.

Beautiful Soup. Библиотека Python для быстрого парсинга HTML- и XML-файлов.

scrape. Модуль Python для веб-браузинга и скрапинга.

mechanize. Очень полезный модуль, благодаря которому вы получаете эмулятор браузера для взаимодействия с веб-страницами.

libgmail. Обеспечивает доступ к гугловскому сервису Gmail.

Google Maps. Благодаря этому модулю можно использовать веб-сервисы платформы Google Maps в своем приложении на Python.

Requests позволяет невероятно легко отсылать HTTP/1.1-запросы.

Selenium. При помощи этого модуля разработчики могут программными методами открывать веб-страницы, заполнять поля, кликать по кнопкам и отсылать формы.

pyquery позволяет делать jQuery-запросы в XML-документах. API этой библиотеки максимально приближен к jQuery. Для быстрой манипуляции с XML и HTML pyquery использует LXML.

Компиляция файлов

Для ускорения запуска программ, использующих большое количество модулей, если уже существует файл с именем my_module.pyc в том же каталоге, где найден my_module.py, считается, что он содержит байт-компилированный модуль my_module. Если такого файла нет, то он создается, и время последнего изменения my_module.py записывается в созданном my_module.pyc. Содержимое байт-компилированных файлов является платформенно-независимым (но может быть разным для разных версий интерпретатора), так что каталог с модулями может совместно использоваться машинами с разными архитектурами.

Некоторые полезные опции компиляции:

1. — эта опция заставляет интерпретатор компилировать так называемый оптимизированный байт-код и сохранять его в файле с расширением ‘.pyo’. При этом из кода удаляются ассерты, игнорируется условный дебаг, ‘.pyc’-файлы игнорируются.
2. — эта опция делает то же, что и предыдущая опция, плюс удаляет комменты.
3. Файл, запускаемый непосредственно из командной строки, никогда не компилируется. Для оптимизации его запуска необходимо большую часть кода убрать в модули.
4. Модуль может загружаться из файлов с расширением ‘.pyс’ или ‘.pyo’, даже если нет файла с расширением ‘.py’. Это может пригодиться в тех случаях, когда вы не хотите распространять исходный код.
5. Кроме того, интерпретатор может загружать бинарники, собранные с помощью языка си — файлы с расширением ‘.so’ в линуксе либо ‘.dll’ в Windows.
6. Модуль можно «зазипповать» в архив с расширением ‘.zip’ и импортировать из архива.
7. Может быть загружен Java-класс, собранный с помощью Jython.

cmath[править]

Этот модуль всегда доступен и позволяет проводить операции над комплексными числами. При этом функции модуля поддерживают работу не только с комплексными, но и с целыми числами и числами с плавающей запятой

Причина, по которой имеются два таких схожих модуля, в том, что многим пользователям не нужны комплексные числа или они просто не знают что это такое. В этих случаях будет даже лучше, если при math.sqrt(-1) будет возбуждено исключение, чем будет найдено комплексное решение. При этом отметим, что функции в модуле всегда возвращают комплексное число, даже если исходные числа не содержат мнимой части.

Переход к полярным координатам и обратноправить

Комплексное число z может быть представлено в Декартовой системе координат в представлении, что действительная z.real часть откладывается по оси x, а мнимая z.imag — по оси y. Само число z записывается:

z = z.real + z.imag*1j

Полярные координаты позволяют представить комплексное число другим образом — в виде радиуса ρ и фазового угла φ. Координата ρ определяет расстояние от точки до полюса, координата φ — угол между полярной осью и отрезком, соединяющим полюс и рассматриваемую точку.

Следующие функции могут быть использованы для перехода от исходных прямоугольных координат к полярным:

• cmath.phase

  Возвращает фазовый угол φ для числа x, phase(x) эквивалентно math.atan2(x.imag, x.real). Результат лежит в интервале .

  (x)

• cmath.polar

  Возвращает представление x в полярных координатах, то есть возвращает пару (r, phi).

  (x)

• cmath.rect(r, phi)

  Возвращает обычное комплексное представление x из представления в полярных координатах.

  (x)

Другие функцииправить

Модуль содержит также ряд функций, с которыми мы ознакомились в модуле math, имеющими то же применение не только к действительным, но и к комплексным числам:

Константыправить

• cmath.pi
• cmath.e

Изучив, данный раздел, мы можем приступить к третьему уроку данного курса, посвященному циклу и последовательностям.

Getting to Know the Python math Module

The Python module is an important feature designed to deal with mathematical operations. It comes packaged with the standard Python release and has been there from the beginning. Most of the module’s functions are thin wrappers around the C platform’s mathematical functions. Since its underlying functions are written in CPython, the module is efficient and conforms to the C standard.

The Python module offers you the ability to perform common and useful mathematical calculations within your application. Here are a few practical uses for the module:

• Calculating combinations and permutations using factorials
• Calculating the height of a pole using trigonometric functions
• Calculating radioactive decay using the exponential function
• Calculating the curve of a suspension bridge using hyperbolic functions
• Solving quadratic equations
• Simulating periodic functions, such as sound and light waves, using trigonometric functions

Since the module comes packaged with the Python release, you don’t have to install it separately. Using it is just a matter of importing the module:

>>>

Библиотека Statsmodel в Python

С помощью пакета Statsmodel можно выполнять статистические вычисления, которые включают в себя описательную статистику, логический вывод, а также оценку для различных статистических моделей. Это способствует эффективному статистическому исследованию данных.

Ниже приведен пример реализации библиотеки Statsmodel в Python.

Python

import numpy as np
import statsmodels.api as sm
import statsmodels.formula.api as smf

input_data = sm.datasets.get_rdataset(«Guerry», «HistData»).data

res = smf.ols(‘Lottery ~ Literacy + np.log(Pop1831)’, data = input_data).fit()
print(res.summary())

1 2 3 4 5 6 7 8 9

importnumpy asnp importstatsmodels.api assm importstatsmodels.formula.api assmf input_data=sm.datasets.get_rdataset(«Guerry»,»HistData»).data res=smf.ols(‘Lottery ~ Literacy + np.log(Pop1831)’,data=input_data).fit() print(res.summary())

Логические операции с десятичным модулем

Decimal содержит набор встроенных функций для выполнения логических операций с десятичными числами, таких как AND, OR, XOR и т. Д.

• Функция logical_and(): выполняет операцию логического И над двумя десятичными числами и возвращает результат.
• Функция logical_or(): выполняет операцию логического ИЛИ над двумя десятичными числами и возвращает результат.
• Функция logical_xor(): выполняет логическую операцию XOR над двумя десятичными числами и возвращает результат.

#Syntax for logical_and() function-
decimal1.logical_and(decimal2)

#Syntax for logical_or() function-
decimal1.logical_or(decimal2)

#Syntax for logical_xor() function-
decimal1.logical_xor(decimal2)

Пример:

import decimal as d

valx = d.Decimal(1001)
valy = d.Decimal(1111)

print("Value 1: ",valx)
print("Value 2: ",valy)

AND = valx.logical_and(valy)
print("The logical AND value of the two decimals: ",AND)

OR = valx.logical_or(valy)
print("The logical OR value of the two decimals: ",OR)

XOR = valx.logical_xor(valy)
print("The logical XOR value of the two decimals: ",XOR)

Выход:

Value 1:  1001
Value 2:  1111
The logical AND value of the two decimals:  1001
The logical OR value of the two decimals:  1111
The logical XOR value of the two decimals:  110

Линейная алгебра

Матрицы

Матрицы в создаются как экземпляры класса :

sym.Matrix(, ])

В отличие от , мы можем использовать в матрицах символьные переменные:

x, y = sym.symbols('x, y')
A = sym.Matrix(, ])
A

И производить с ними разные манипуляции:

A**2

Дифференциальные уравнения

При помощи библиотеки SymPy можно решать некоторые обыкновенные дифференциальные уравнения. Для этого используется функция . Для начала нам надо задать неопределенную функцию. Это можно сделать, передав параметр в функцию .

f, g = sym.symbols('f g', cls=sym.Function)

Теперь и заданы как неопределенные функции. мы можем в этом убедиться, просто вызвав .

f(x) # результат ?(?)
f(x).diff(x, x) + f(x)

Теперь решим следующее дифференциальное уравнение:

sym.dsolve(f(x).diff(x, x) + f(x), f(x))
# результат ?(?)=?1sin(?)+?2cos(?)

Чтобы улучшить решаемость и помочь этой функции в поиске решения, можно передавать в нее определенные ключевые аргументы. Например, если мы видим, что это уравнение с разделяемыми переменными, то мы можем передать в функцию аргумент .

sym.dsolve(sym.sin(x) * sym.cos(f(x)) + sym.cos(x) * sym.sin(f(x)) * f(x).diff(x), f(x), hint='separable') 
# результат [Eq(f(x), -acos(C1/cos(x)) + 2*pi), Eq(f(x), 
#            acos(C1/cos(x)))]

Манипуляции с изображениями и видео

Python это очень мощный язык; с его помощью
можно решать многие задачи, например,
работать с изображениями. Стандартная
библиотека не имеет встроенного
функционала для этих целей, но следующие
модули вам помогут.

Python Imaging Library (PIL). PIL добавляет в интерпретатор Python возможность обработки изображений. Эта библиотека поддерживает много форматов файлов и предоставляет хороший функционал для работы с графикой.

Gdmodule. Это интерфейс для библиотеки GD, созданной Томасом Баутелом.

VideoCapture. Win32-расширение для доступа к таким видеоустройствам, как веб-камеры (USB) и ТВ-карты.

MoviePy. Библиотека Python для редактирования видео: обрезка, склейка, вставка надписей, нелинейное редактирование, обработка видео и создание пользовательских эффектов.

pyscreenshot. Кроссплатформенный модуль, позволяющий делать скриншоты без установки сторонних библиотек.

Фаза (аргумент)

Мы можем представить комплексное число как вектор, состоящий из двух компонентов на плоскости, состоящей из и осей. Следовательно, две составляющие вектора — это действительная и мнимая части.

Угол между вектором и действительной осью определяется как или комплексного числа.

Формально это определяется как:

фаза (число) = arctan (мнимая_часть / действительная_часть)

где функция arctan является обратной математической функцией tan.

В Python мы можем получить фазу комплексного числа, используя модуль для комплексных чисел. Мы также можем использовать функцию и получить фазу из ее математического определения.

import cmath
import math

num = 4 + 3j

# Using cmath module
p = cmath.phase(num)
print('cmath Module:', p)

# Using math module
p = math.atan(num.imag/num.real)
print('Math Module:', p)

Вывод:

cmath Module: 0.6435011087932844
Math Module: 0.6435011087932844

Обратите внимание, что эта функция возвращает фазовый угол в , поэтому, если нам нужно преобразовать в , мы можем использовать другую библиотеку, например

import cmath
import numpy as np

num = 4 + 3j

# Using cmath module
p = cmath.phase(num)
print('cmath Module in Radians:', p)
print('Phase in Degrees:', np.degrees(p))

Вывод:

cmath Module in Radians: 0.6435011087932844
Phase in Degrees: 36.86989764584402

cmath vs math

A complex number is a combination of a real number and an imaginary number. It has the formula of a + bi, where a is the real number and bi is the imaginary number. Real and imaginary numbers can be explained as follows:

• A real number is literally any number you can think of.
• An imaginary number is a number that gives a negative result when squared.

A real number can be any number. For example, 12, 4.3, -19.0 are all real numbers. Imaginary numbers are shown as i. The following image shows an example of a complex number:

In the example above, 7 is the real number and 3i is the imaginary number. Complex numbers are mostly used in geometry, calculus, scientific calculations, and especially in electronics.

The functions of the Python module aren’t equipped to handle complex numbers. However, Python provides a different module that can specifically deal with complex numbers, the module. The Python module is complemented by the module, which implements many of the same functions but for complex numbers.

You can import the module as follows:

>>>

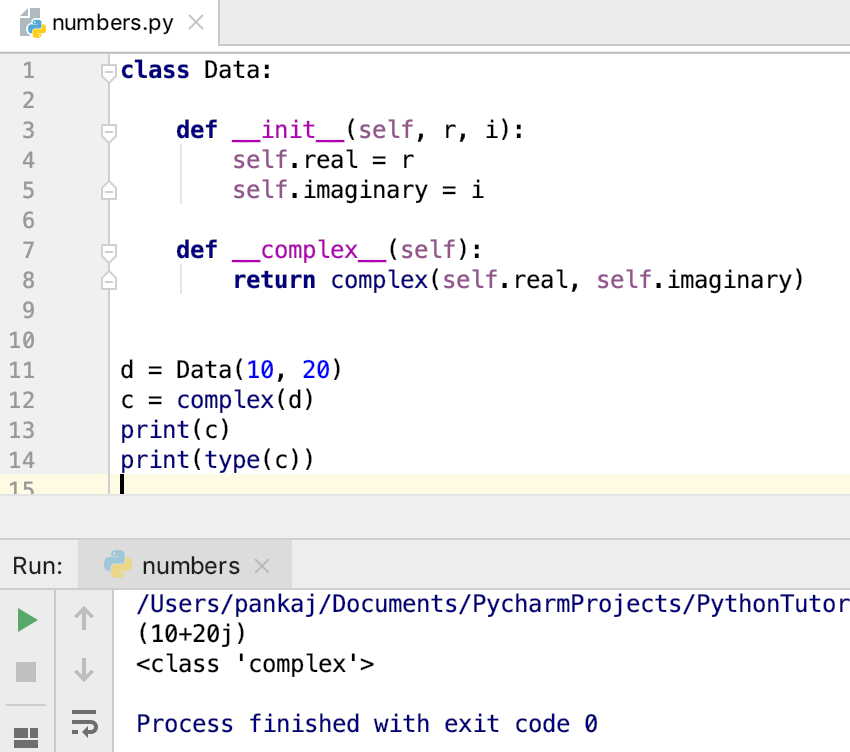
Since the module is also packaged with Python, you can import it the same way you imported the module. Before you work with the module, you have to know how to define a complex number. You can define a complex number as follows:

>>>

As you can see, you can determine that a number is indeed complex by using .

Note: In mathematics, the imaginary unit is usually denoted i. In some fields, it’s more customary to use j for the same thing. In Python, you use to denote imaginary numbers.

Python also provides a special built-in function called that lets you create complex numbers. You can use as follows:

>>>

You can use either method to create complex numbers. You can also use the module to calculate mathematical functions for complex numbers as follows:

>>>

Комбинации элементов между собой

В библиотеке есть еще одна функция, связанная с перестановками и комбинациями, называемая . Эта функция является разновидностью функции , с той небольшой разницей, что она включает комбинации элементов между собой.

import itertools

values = 

com = itertools.combinations_with_replacement(values, 2)

for val in com:
	print(*val)

Выход:

1 1
1 2
1 3
1 4
2 2
2 3
2 4
3 3
3 4
4 4

Мы можем видеть четкое отличие вышеприведенного вывода от вывода с теми же параметрами при передаче в функцию .

Есть комбинации чисел, как будто их несколько экземпляров в списке. В основном это происходит потому, что, когда мы выбираем элемент из списка, вышеуказанная функция снова помещает то же значение, чтобы получить комбинации.

Еще пример. Наша задача — отобразить перестановку заданной строки. Здесь решаем эту проблему в python, используя перестановки встроенных функций (итерируемые).

Input : string = 'XYZ'
Output : XYZ
         XZY 
         YXZ
         YZX
         ZXY       
         ZYX

Алгоритм

Step 1: given string.
Step 2: Get all permutations of string.
Step 3: print all permutations.

Пример кода

from itertools import permutations 
def allPermutations(str1): 
   # Get all permutations of string 'ABC' 
   per = permutations(str1) 
   # print all permutations
   print("Permutation Of this String ::>")
   for i in list(per): 
      print (''.join(i)) 
# Driver program 
if __name__ == "__main__": 
   str1 = input("Enter the string ::>")
   allPermutations(str1) 

Вывод

Enter the string ::> abc
Permutation Of this String ::>
abc
acb
bac
bca
cab
cba

Импорт модуля

Если запустить в каталоге, в котором лежит данный модуль (например, my_module.py), интерпретатор:

>>> python

и потом сделать импорт модуля:

>>> import my_module

то мы получаем доступ ко всем функциям, которые в модуле определены:

>>> my_module.func1()
>>> my_module.func2()
...

Для более короткой записи можно создать локальную переменную:

>>> f1 = my_module.func1

Второй вариант импорта — взятие непосредственно имени без имени модуля:

>>> from my_module import func1, func2
>>> func1()

Третий вариант импорта — включение всех имен, определенных в модуле:

>>> from my_module import *
>>> func1()

Для предотвращения конфликта имен можно использовать создание алиаса:

>>> from my_module import open as my_open

Пример. Импорт на основе from обладает такой особенностью, что он делает импортируемые атрибуты read-only:

>>> from small import x, y
>>> x = 42

В данном случае x — это локальная переменная, в то время как переменные x, y в самом модуле small не меняются:

>>> import small
>>> small.x = 42

здесь x — глобальная переменная.

Во избежание недоразумений import предпочтительнее без from в тех случаях, когда один и тот же модуль используется в нескольких местах.

Поскольку модуль загружается один раз, для его повторной загрузки можно использовать функцию reload().

Каждый модуль имеет собственное пространство имен, являющееся глобальной областью видимости для всех определенных в нем функций. Для того чтобы переменные этого модуля не попали в конфликт с другими глобальными именами или другими модулями, нужно использовать префикс: _имя_модуля_._имя_переменной_ .

Модули могут импортировать другие модули. Обычно инструкцию import располагают в начале модуля или программы.

Operator Precedence

In Python, as in mathematics, we need to keep in mind that operators will be evaluated in order of precedence, not from left to right or right to left.

If we look at the following expression:

We may read it left to right, but remember that multiplication will be done first, so if we call , we will receive the following value:

This is because evaluates to , and then we add to return as the final result.

If instead we would like to add the value to , then multiply that sum by , we can use parentheses just like we would in math:

One way to remember the order of operation is through the acronym PEMDAS:

Order	Letter	Stands for
1	P	Parentheses
2	E	Exponent
3	M	Multiplication
4	D	Division
5	A	Addition
6	S	Subtraction

You may be familiar with another acronym for the order of operations, such as BEDMAS or BODMAS. Whatever acronym works best for you, try to keep it in mind when performing math operations in Python so that the results that you expect are returned.

Addition and Subtraction

In Python, addition and subtraction operators perform just as they do in mathematics. In fact, you can use the Python programming language as a calculator.

Let’s look at some examples, starting with integers:

Instead of passing integers directly into the statement, we can initialize variables to stand for integer values:

Because integers can be both positive and negative numbers (and 0 too), we can add a negative number with a positive number:

Addition will behave similarly with floats:

Because we added two floats together, Python returned a float value with a decimal place.

The syntax for subtraction is the same as for addition, except you’ll change your operator from the plus sign () to the minus sign ():

Here, we subtracted an integer from a float. Python will return a float if at least one of the numbers involved in an equation is a float.

Как сделать и вставить гиперссылку на слайд в презентации — примеры оформления

Арифметические операции

Подобно действительным числам, комплексные числа также можно складывать, вычитать, умножать и делить. Давайте посмотрим, как мы могли бы это сделать в Python.

a = 1 + 2j
b = 2 + 4j
print('Addition =', a + b)
print('Subtraction =', a - b)
print('Multiplication =', a * b)
print('Division =', a / b)

Выход:

Addition = (3+6j)
Subtraction = (-1-2j)
Multiplication = (-6+8j)
Division = (2+0j)

ПРИМЕЧАНИЕ. В отличие от действительных чисел, мы не можем сравнивать два комплексных числа. Мы можем сравнивать только их действительную и мнимую части по отдельности, поскольку это действительные числа. Приведенный ниже фрагмент доказывает это.

>>> a
(4+3j)
>>> b
(4+6j)
>>> a < b
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
TypeError: '<' not supported between instances of 'complex' and 'complex'

Multiplication and Division

Like addition and subtraction, multiplication and division will look very similar to how they do in mathematics. The sign we’ll use in Python for multiplication is and the sign we’ll use for division is .

Here’s an example of doing multiplication in Python with two float values:

When you divide in Python 3, your quotient will always be returned as a float, even if you use two integers:

This is one of the . Python 3’s approach provides a fractional answer so that when you use to divide by the quotient of will be returned. In Python 2 the quotient returned for the expression is .

Python 2’s operator performs floor division, where for the quotient the number returned is the largest integer less than or equal to . If you run the above example of with Python 2 instead of Python 3, you’ll receive as the output without the decimal place.

In Python 3, you can use to perform floor division. The expression will return the value of . Floor division is useful when you need a quotient to be in whole numbers.

Гиперболические функции

Подобно тригонометрическим функциям, гиперболические функции для комплексного числа также доступны в модуле .

import cmath

a = 3 + 4j

print('Hyperbolic Sine:', cmath.sinh(a))
print('Hyperbolic Cosine:', cmath.cosh(a))
print('Hyperbolic Tangent:', cmath.tanh(a))

print('Inverse Hyperbolic Sine:', cmath.asinh(a))
print('Inverse Hyperbolic Cosine:', cmath.acosh(a))
print('Inverse Hyperbolic Tangent:', cmath.atanh(a))

Вывод:

Hyperbolic Sine: (-6.5481200409110025-7.61923172032141j)
Hyperbolic Cosine: (-6.580663040551157-7.581552742746545j)
Hyperbolic Tangent: (1.000709536067233+0.00490825806749606j)
Inverse Hyperbolic Sine: (2.2999140408792695+0.9176168533514787j)
Inverse Hyperbolic Cosine: (2.305509031243477+0.9368124611557198j)
Inverse Hyperbolic Tangent: (0.11750090731143388+1.4099210495965755j)

Библиотека Math в Python

Math является самым базовым математическим модулем Python. Охватывает основные математические операции, такие как сумма, экспонента, модуль и так далее. Эта библиотека не используется при работе со сложными математическими операциями, такими как умножение матриц. Расчеты, выполняемые с помощью функций библиотеки math, также выполняются намного медленнее. Тем не менее, эта библиотека подходит для выполнения основных математических операций.

Пример: Вы можете найти экспоненту от 3, используя функцию библиотеки math следующим образом:

Python

from math import exp
exp(3) # Вычисление экспоненты

1 2	frommathimportexp exp(3)# Вычисление экспоненты

Data Science и математика

Для Python есть много расширений, которые
можно использовать в научных целях,
например, в математике, науке о данных
и инженерии.

SciPy. SciPy (произносится как «сай пай») это экосистема программного обеспечения с открытым кодом для математики, науки и инженерии.

Matplotlib. Библиотека Python для создания 2D-графиков. Генерирует пригодные для печати изображения в разных форматах. Matplotlib может использоваться в скриптах, интерпретаторе Python, в Jupyter Notebook, на серверах веб-приложений и в GUI-инструментарии.

Pandas. Быстрый, мощный, гибкий и легкий в использовании инструмент для анализа данных и работы с данными. Имеет открытый исходный код.

Numpy. Библиотека, обеспечивающая поддержку больших, многомерных массивов и матриц. Для работы с этими массивами Numpy имеет обширную коллекцию высокоуровневых математических функций.

Операции над числами

Манипуляции над числовыми значениями в языке программирования Python выполняются благодаря множеству различных операций, символьные обозначения которых, как правило, совпадают с аналогами из традиционной математики. Таким образом, можно прибавлять, отнимать, умножать, делить, находить остаток от деления и возводить в степень числовые значения любых разновидностей. Ознакомиться с основными типами операций, которые выполняются над цифровыми значениями, можно из следующей небольшой таблицы:

Операция	Назначение
a + b	Сложение a и b
a – b	Разница между a и b
a * b	Умножение a на b
a / b	Деление a на b
a % b	Остаток от деления a на b
a // b	Целая часть от деления a и b
a ** b	Возведение a в степень b

Помимо вышеперечисленных арифметических действий, над числами можно осуществлять битовые операции, которые задействуют их двоичное представление. Перечень подобных операций представлен в следующей таблице, где можно найти назначение каждой из них:

Операция	Назначение
a & b	Побитовое И для a и b
a | b	Побитовое ИЛИ для a и b
a ^ b	Исключающее ИЛИ для a и b
~a	Инверсия битов для a
a << b	Побитовый сдвиг влево для a на b
a >> b	Побитовый сдвиг вправо для a на b

Также для более эффективной обработки числовых данных в Python были добавлены особые методы, позволяющие всего за одно действие осуществлять множество сложных операций. К наиболее популярным из них относятся методы, предназначенные для быстрого нахождения квадратного корня, модуля, а также округления числа. Чтобы воспользоваться некоторыми арифметическими функциями, необходимо подключить стандартную библиотеку math при помощи вызова . Список популярных методов представлен в данной таблице:

Метод	Назначение
sqrt(a)	Квадратный корень из a
log(a)	Натуральный логарифм из a
fabs(a)	Возвращает модуль a
round(a)	Округляет a до ближайшего целого
round(a, b)	Округляет a до b знаков после точки
floor(a)	Округляет a до меньшего целого значения
ceil(a)	Округляет a до большего целого значения
isfinite(a)	Проверяет, является ли a числом
modf(a)	Возвращает целую и дробную части a
sin(a)	Синус угла a, указанного в радианах
cos(a)	Косинус угла a, указанного в радианах
tan(a)	Тангенс угла a, указанного в радианах

Функция fabs модуля math вначале пытается привести аргумент к вещественному типу (float), и только потом вычисляет модуль. Для вычисления модуля числа так же есть стандартная функция abs.

Ввод числа с клавиатуры

Для того чтобы получить числовые данные от пользователя используется стандартный метод input. Его вызов позволяет получать ввод информации с клавиатуры, который выполняется во время запуска программы на компьютере. В качестве аргумента для этого метода можно использовать строку, предлагающую пользователю ввести числовые сведения. Ниже показан пример того, как ввести в Pyhon с клавиатуры число. Переменная n получает значение и отображается на экране с помощью print:

n = input("Press n: ")
print("n = " + str(n))

Press n: 10
n = 10

Максимальное значение

Получить максимальное значение целочисленной переменной, которое поддерживается в текущей версии языка Python можно с помощью переменной sys.maxsize. Как правило, на разных компьютерах это число совпадать не будет из-за разной архитектуры процессоров. На данный момент из Python были убраны любые ограничения, касающиеся размерности вводимых величин. Вывести на экран максимальное число в Python можно следующим образом:

import sys
print(sys.maxsize)

9223372036854775807

Тригонометрические функции

Тригонометрические функции для комплексного числа также доступны в модуле .

import cmath

a = 3 + 4j

print('Sine:', cmath.sin(a))
print('Cosine:', cmath.cos(a))
print('Tangent:', cmath.tan(a))

print('ArcSin:', cmath.asin(a))
print('ArcCosine:', cmath.acos(a))
print('ArcTan:', cmath.atan(a))

Вывод:

Sine: (3.853738037919377-27.016813258003936j)
Cosine: (-27.034945603074224-3.8511533348117775j)
Tangent: (-0.0001873462046294784+0.999355987381473j)
ArcSin: (0.6339838656391766+2.305509031243477j)
ArcCosine: (0.9368124611557198-2.305509031243477j)
ArcTan: (1.4483069952314644+0.15899719167999918j)

Как отфильтровать элементы с помощью takewhile() и drop while()

Мы можем использовать Python для фильтрации элементов последовательности, если условие . Если условие становится , фильтрация прекращается.

iterator = itertools.takewhile(condition, *sequence)

Вот простой пример, который фильтрует числа, если число положительное.

import itertools

sequence = itertools.takewhile(lambda x: x > 0, )

for item in sequence:
    print(item)

Выход

1
2
3

Здесь последовательность остановилась после 3, поскольку следующий элемент равен -1.

Точно так же фильтрует элементы, пока условие имеет значение и возвращает все элементы после первого значения, отличного от false.

import itertools

data = itertools.dropwhile(lambda x: x < 5, )
for item in data:
    print(item)

Выход

12
7
1
-5

Заключение

Сегодня мы узнали основы модульной системы питона и импорта компонентов. Импорт модулей — это основа программной архитектуры в питоне. Большие программы состоят из большого количества файлов, и объединяет их линковка во время исполнения на основе импорта. Модули структурируют программу, разбивая логику на отдельные компоненты. Код внутри одного модуля изолирован от остальных модулей, что минимизирует коллизию имен внутри программы.

Пакетный импорт упрощает поиск путей, на уровне файловой системы организует управление модульными библиотеками с многоуровневой вложенностью. В продолжение цикла мы расскажем о классах в Python. Код примеров проверялся на версии питона 2.6.

<< Предыдущая статья. Следующая статья >>