Функции для работы с матрицами в excel

Формулы массива в Excel

Под массивом обычно понимают набор данных, объединенных в группу. Массивы бывают одномерные (элементы массива образуют строку или столбец) или двумерные (матрица). Легко сообразить, что почти в любой таблице Excel при желании можно найти один или несколько таких массивов:

Формулы массива в Excel – это специальные формулы для обработки данных из таких массивов. Формулы массива делятся на две категории – те, что возвращают одно значение и те, что дают на выходе целый набор (массив) значений. Рассмотрим их на простых примерах…

Пример 1. Классика жанра – товарный чек

Задача: рассчитать общую сумму заказа. Если идти классическим путем, то нужно будет добавить столбец, где перемножить цену и количество, а потом взять сумму по этому столбцу. Если же применить формулу массива, то все будет гораздо красивее:

1. выделяем ячейку С7
2. вводим с клавиатуры =СУММ(
3. выделяем диапазон B2:B5
4. вводим знак умножения (звездочка)
5. выделяем диапазон C2:C5 и закрываем скобку функции СУММ – в итоге должно получиться так:
6. чтобы Excel воспринял нашу формулу как формулу массива жмем не Enter, как обычно, а Ctrl + Shift + Enter

Вуаля!

Т.е. Excel произвел попарное умножение элементов массивов B2:B5 и C2:C5 и образовал новый массив стоимостей (в памяти компьютера), а затем сложил все элементы этого нового массива.

Обратите внимание на фигурные скобки, появившиеся в формуле – отличительный признак формулы массива. Вводить их вручную с клавиатуры бесполезно – они автоматически появляются при нажатии Ctrl + Shift + Enter

Пример 2. Разрешите Вас… транспонировать?

При работе с таблицами часто возникает необходимость поменять местами строки и столбцы, т.е. развернуть таблицу на бок, чтобы данные, которые раньше шли по строке, теперь располагались в столбцах и наоборот. В математике такая операция называется транспонированием. При помощи формулы массива и функции ТРАНСП (TRANSPOSE) это делается на раз.

Допустим, имеем двумерный массив ячеек, который хотим транспонировать.

• Выделяем диапазон ячеек для размещения транспонированной таблицы. Поскольку исходный массив ячеек был 8 строк на 2 столбца, то надо выделить диапазон пустых ячеек размером 2 строки на 8 столбцов.
• вводим функцию транспонирования =ТРАНСП(   
• в качестве аргумента функции выделяем наш массив ячеек A1:B8

жмем Ctrl + Shift + Enter и получаем “перевернутый массив” в качестве результата:

Редактирование формулы массива

Если формула массива расположена не в одной ячейке (как в Примере 1), а в нескольких ячейках (как в Примере 2), то Excel не позволит редактировать или удалить одну отдельно взятую формулу (например в ячейке D10) и выдаст предупреждающее сообщение Невозможно изменить часть массива.

Для редактирования формулы массива необходимо выделить весь диапазон (A10:H11 в нашем случае) и изменить формулу в строке формул (или нажав F2). Затем необходимо повторить ввод измененной формулы массива, нажав сочетание клавиш Ctrl + Shift + Enter.

Excel также не позволит свободно перемещать ячейки, входящие в формулу массива или добавлять новые строки-столбцы-ячейки в диапазон формулы массива (т.е. в диапазон A10:H11 в нашем случае)

Пример 3. Таблица умножения

Вспомните детство, школу, свою тетрадку по математике… На обороте тетради на обложке было что? Таблица умножения вот такого вида:

При помощи формул массива она вся делается в одно движение:

1. выделяем диапазон B2:K11
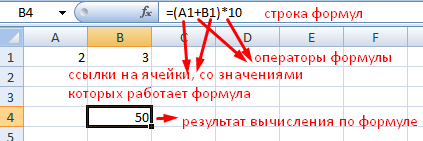
2. вводим формулу =A2:A11*B1:K1
3. жмем Ctrl + Shift + Enter, чтобы Excel воспринял ее как формулу массива

и получаем результат:

Пример 4. Выборочное суммирование

Посмотрите как при помощи одной формулы массива красиво и легко выбираются данные по определенному товару и заказчику:

 В данном случае формула массива синхронно пробегает по всем элементам диапазонов C3:C21 и B3:B21, проверяя, совпадают ли они с заданными значениями из ячеек G4 и G5. Если совпадения нет, то результат равенства ноль, если совпадение есть, то единица. Таким образом суммы всех сделок, где заказчик не ANTON и товар не Boston Crab Meat умножаются на ноль и суммируются только нужные заказы.

2.8. Критическая ошибка в Excel 2003

В Excel 2003 функции TREND и
LINEST при определенных
условиях дают неверный результат.

Так происходит когда одновременно:

• среднее значение по каждой переменной в матрице
  предикторов X равно нулю;

• среднее значение отклика Y
  не равно нулю.

На показан как раз такой
случай: средние значения по всем столбцам матрицы Xc
равны нулю, а среднее по столбцу Yc отлично от нуля..

Пример 
 

Рис.37 Ошибка в регрессионных функциях Excel
2003

Ситуацию можно исправить, применяя функцию
TREND к
центрированным значениям отклика, с последующей коррекцией результата.
Для этого можно использовать формулу
=TREND(Yc-ym,
Xc)+ym, применение которой показано на том же рисунке.

Удивительно, но эта ошибка не была замечена
пользователями. Однако в новой версии 2007 она исправлена.  

Векторизуем внутренний цикл (2-й шаг)

1. Компиляторы нынче умные пошли (не все!), и вполне справляются с задачей автовекторизации простых циклов. Уже в 1-м варианте компилятор фактически задействовал инструкции AVX2/FMA, потому ручная оптимизация не дала нам практически никаких преимуществ.
2. Скорость расчетов в данном случае упирается не в вычислителные возможности процессора, а в скорость загрузки и выгрузки данных. В данном случае процессору для задействования 2 256-bit FMA блоков требуется загрузить 4 и выгрузить 2 256-bit вектора за такт. Это в два раза превышает даже пропускную способность L1 кеша процессора (512/256 bit), не говоря уже о пропускной способности памяти, которая еще на порядок меньше (64-bit на канал)).

3 .3 . Пример макроса

Второй способ опирается на рекуррентное соотношение,
связывающее два соседних члена в ряду

Для того чтобы воспользоваться этим соотношением, надо
организовать на листе рекуррентную процедуру. Например, так, как
показано на Рис. 42

Рис.42
Вычисление функции E
1 (x
)
итерационным способом

Один шаг итерации – это переход от значений в области
J2:J4
к значениям в области
L2:L4
. Для того, чтобы сделать следующую
итерацию, нужно скопировать значения, получившиеся в области
L2:L4
и вставить их в область
J2:J4
. При этом вставлять нужно только
величины, без формул. Величины в области H2:H4

дают исходные значения для начала итерации.Повторяя многократно
операцию Copy-Paste Special
, можно получить в
ячейке L4
искомое значение. Однако
копирование – это скучное занятие и его было бы неплохо
автоматизировать. Для этого можно написать макрос.

Проще всего начать создание макроса через запись команд,
выполняемых на листе. Для этого идем в раздел меню Tools–Macro–Record
New Macro
. Появляется окно (Рис. 43
), в котором можно указать имя
макроса и где он будет расположен.

Рис.43
Запись макро

После нажатия OK
начинается
запись всех действий, выполняемых на листе. Когда все, что нужно
сохранено в макросе, запись надо остановить командой
Tools–Macro–Stop Recording
. Результат можно увидеть, зайдя в
редактор Visual Basic

.

Рис.44
Редактор Visual Basic

На Рис.

Рис.45
Функция IntExp

На Рис. 45
приведен
код этой функции и пример обращения к
ней.

Мы не будем рассказывать о программировании на VBA, т.к.
это очень большой и сложный вопрос. Самостоятельно его можно изучить по
имеющимся в сети многочисленным пособиям, например,
.

VBA – это довольно медленный язык и он плохо подходит
для больших вычислений. Например, не стоит писать на этом языке
процедуру для PCA декомпозиции – на больших массивах она будет считать
очень долго. Правильнее рассматривать Excel и VBA как интерфейс (front
end) для ввода и вывода данных, которые затем передаются в динамическую
библиотеку (DLL), написанную на быстром языке, таком как C++ (back end).
Именно эта концепция и была реализована в надстройках
Fitter
и
Chemometrics
.

Подробнее об использовании пользовательских функций для
расширения возможностей надстройки Chemometrics

можно прочитать
.

1.2. Книга, лист и ячейка

Файл Excel с расширением XLS (XLSX в версии 2007) называется
(рабочей) книгой. Если запустить программу Excel, например, щелкнуть на
рабочем столе иконку
,
то откроется новая пустая книга. . 

Рис. 2 Новая книга Excel

Если рабочая книга уже существует, то ее проще открыть через проводник. Для
этого достаточно щелкнуть по иконке файла.  

Рис. 3
Открытие книги Excel через проводник

Рабочая книга состоит из нескольких листов, имена которых
показаны в нижней части окна. Листы можно удалять, добавлять,
переименовывать. Для этого надо щелкнуть правой клавишей мышки по имени
листа. Появится меню, из которого можно выбрать нужную операцию.

Рис.
4 Операции с листами

Стандартное имя листа – Sheet1, но ему можно дать любое имя, например
Data. На лист можно вставлять рисунки, графики и другие необходимые
объекты.

Каждый лист состоит из ячеек, образующих таблицу, размером 256
столбцов и 65536 строк (В версии 2007 – 16384 столбцов и1048576 строк).
Строки на листе обозначены числами: 1,2, 3…, а столбцы имеют буквенную
кодировку: A, B, …,Z,
AA, AB .., и т.д. до последнего столбца
IV (в 2007
– до XFD). Этот стиль адресации называется A1. Реже применяется
альтернативный стиль R1C1, в котором столбцы также нумеруются. Мы не
будем использовать этот стиль, а прочитать об этом можно

здесь

Строки и столбцы можно удалять, добавлять, прятать, а также менять их размер:
высоту или ширину.

Все операции на листе выполняются с помощью меню, представленного в
верхней части окна (). Меню в Excel 2007
существенно отличается от прежней версии. Там, вместо обычных иконок,
появилась лента. Мы не будем подробно разбирать отличия версий. Те, кому
это интересно могут прочитать

здесь.

Изменение контраста при наведении

Заказать звонок

Присваиваем элементу класс «hover-effect10» и пишем в файле стилей следующее:

PHP

/*Увеличение контрасата*/
.hover-effect10 {
-webkit-transition: all 0.5s ease;
-moz-transition: all 0.5s ease;
transition: all 0.5s ease;
}
.hover-effect10:hover {
-webkit-filter: contrast(185%);
}

1 2 3 4 5 6 7 8 9 10 11

/*Увеличение контрасата*/   .hover-effect10{ -webkit-transitionall0.5sease; -moz-transitionall0.5sease; transitionall0.5sease; }   .hover-effect10hover{ -webkit-filtercontrast(185%); }

Для этого эффекта нам понадобится свойство -webkit-filter: contrast(185%);

Значение контраста указывается в скобках в процентах.

Выполнение расчетов

Вычисление обратной матрицы в Excel возможно только в том случае, если первичная матрица является квадратной, то есть количество строк и столбцов в ней совпадает. Кроме того, её определитель не должен быть равен нулю. Для вычисления применяется функция массива МОБР. Давайте на простейшем примере рассмотрим подобное вычисление.

Расчет определителя

Прежде всего, вычислим определитель, чтобы понять, имеет первичный диапазон обратную матрицу или нет. Это значение рассчитывается при помощи функции МОПРЕД.

1. Выделяем любую пустую ячейку на листе, куда будут выводиться результаты вычислений. Жмем на кнопку «Вставить функцию», размещенную около строки формул.
2. Запускается Мастер функций. В перечне записей, который он представляет, ищем «МОПРЕД», выделяем этот элемент и жмем на кнопку «OK».
3. Открывается окно аргументов. Ставим курсор в поле «Массив». Выделяем весь диапазон ячеек, в котором расположена матрица. После того, как его адрес появился в поле, жмем на кнопку «OK».
4. Программа производит расчет определителя. Как видим, для нашего конкретного случая он равен – 59, то есть не тождественен нулю. Это позволяет сказать, что у данной матрицы существует обратная.

Расчет обратной матрицы

Теперь можно преступить к непосредственному расчету обратной матрицы.

1. Выделяем ячейку, которая должна стать верхней левой ячейкой обратной матрицы. Переходим в Мастер функций, кликнув по значку слева от строки формул.
2. В открывшемся списке выбираем функцию МОБР. Жмем на кнопку «OK».
3. В поле «Массив», открывшегося окна аргументов функции, устанавливаем курсор. Выделяем весь первичный диапазон. После появления его адреса в поле, жмем на кнопку «OK».
4. Как видим, появилось значение только в одной ячейке, в которой была формула. Но нам нужна полноценная обратная функция, поэтому следует скопировать формулу в другие ячейки. Выделяем диапазон, равнозначный по горизонтали и вертикали исходному массиву данных. Жмем на функциональную клавишу F2, а затем набираем комбинацию Ctrl+Shift+Enter. Именно последняя комбинация предназначена для обработки массивов.
5. Как видим, после этих действий обратная матрица вычислена в выделенных ячейках.

На этом расчет можно считать завершенным.

Если вы производите расчет определителя и обратной матрицы только при помощи ручки и бумаги, то над этим вычислением, в случае работы над сложным примером, можно ломать голову очень долго. Но, как видим, в программе Эксель данные вычисления производятся очень быстро, независимо от сложности поставленной задачи. Для человека, который знаком с алгоритмом подобных расчетов в этом приложении, все вычисление сводится к чисто механическим действиям.

Мы рады, что смогли помочь Вам в решении проблемы.

Помогла ли вам эта статья?

Нахождение обратной матрицы всегда вызывало большие затруднения у учащихся, так как это был очень трудоемкий процесс. И вот такое задание вполне по силам EXCEL.  

Прежде всего, уясним одно правило:  Матрица имеет обратную только тогда, когда ее определитель не равен нулю.  А вот и задание: найдите матрицу, обратную к матрице А, где

Вычислять определитель этой матрицы мы умеем. Я его уже вычислил.

Он оказался равен -4, а  это значит, что у нашей матрицы есть обратная (если бы определитель оказался равен нулю, то мы сказали бы что матрица не имеет обратную и немедленно прекратили все вычисления). Теперь отметим ячейку, с которой начнем записывать ответ. Я отметил ячейку E1.  Нажимаем Формулы, затем Математические и в появившемся окне находим  МОБР

После нажатия появляется вот такое окно, в котором надо вписать адреса ячеек, в которых находятся элементы матрицы  в Массив

У нас элементы записаны в ячейки начиная с А1 и заканчивая в С3 , поэтому так и записываем (смотрите картинку)

Если все сделали правильно, то автоматически заполнится место, обведенное красным и запишется ответ, который обведен черным. В таком виде ответ трудно переваривать и поэтому нажимаем ОК.  В ячейке, которую мы застолбили под ответ, появилось число 3,  Это только первый элемент полученной обратной матрицы.

Чтобы виден был весь ответ, выполняем следующие действия: Начиная с  ячейки Е1 выделяем три строчки и три столбца (именно столько было у исходной матрицы и столько же будет у обратной)

нажимаем клавишу F2,  а затем на одновременно на три клавиши  Ctrl+Shift+Enter.

В выделенном месте появляются, теперь уже все, элементы обратной матрицы. Если Вы сохраните этот документ, то в следующий раз можете воспользоваться плодами своего труда. Так, меняя элементы исходной матрицы, Вы автоматически получаете для нее же обратную матрицу.

На этом все. Крепких вам знаний.

Рубрика: EXCEL в помощь, Статьи. Метки: EXCEL, ИКТ, матрица, обратная матрица

2.9. Виртуальный массив

При анализе данных часто возникает проблема сохранения
промежуточных результатов, которые нужны не сами по себе, а только для
того, чтобы вычислить по ним другие, полезные значения. Например,
остатки в методе PCA часто нам не интересны, а нужны только для
определения полной объясненной дисперсии, ортогональных расстояний и
т.п. При этом размеры таких промежуточных массивов могут быть очень
велики, да и к тому же их приходится вычислять при различных значениях
числа главных компонент. Все это ведет к заполнению рабочей книги
большим количеством ненужных, промежуточных результатов. Этого можно
избежать, если использовать виртуальные массивы. Поясним их суть на
простом примере. 

Рис.38 Пример использования виртуального
массива

Предположим, что задана матрица A, а
нужно вычислить детерминант матрицы AtA
. На Рис. 38 показаны два способа вычисления. Первый – через
последовательность промежуточных массивов, отмеченных красными
стрелками. Второй – с помощью одной формулы, показанной зеленой
стрелкой. Оба пути ведут к одному и тому же результату, но красный путь
занимает на листе много места, а зеленый последовательно использует
несколько промежуточных виртуальных массивов. Все они, по сути,
совпадают с реальными массивами красного пути, но на лист не выводятся.

Первый массив –  это транспонированная матрица At,
получаемая как результат функции
(A).

Второй виртуальный массив получается тогда, когда первый
виртуальный массив умножается на матрицу A с помощью
функции (TRANSPOSE(A), A).  

И, наконец, к этому, второму виртуальному массиву применяется функция
.

Виртуальные массивы очень полезны при вычислении всяческих
вспомогательных характеристик в анализе многомерных данных: остатков,
собственных значений, и т.п. Подробно об этом рассказывается в пособии
Расширение возможностей Chemometrics Add-In.

2.7. Регрессия

Для построения используются
несколько стандартных функций листа.

TREND / ТЕНДЕНЦИЯ

Строит

y=b+m₁x₁+…+m_J x_J+e

Аппроксимирует известные значения вектора откликов
known_y’s для заданных значений матрицы предикторов
known_x’s и возвращает значения y,
для заданного массива new_x’s.  

Синтаксис 

TREND(known_y’s
)

Примечания 

• Вектор
  known_y’s должен занимать один столбец,
  тогда каждый столбец матрицы массива known_x’s
  интерпретируется как отдельная переменная;

• Если
  аргумент known_x’sопущен, то предполагается, что это вектор чисел {1;2;3;…}
  такого же размера, как и known_y’s;

• Матрица
  новых значений new_x’sдолжна иметь столько же столбцов
  (переменных), как и матрица known_x’s;

• Если
  аргумент new_x’sопущен, то предполагается, что он совпадает с
  массивом known_x’s.
  Результат является вектором, в котором число строк равно
  числу строк в массиве new_x’s.

Пример 
 

Рис.34 Функция TREND

Функция TRENDявляется функцией
массива и ее ввод должен завершаться нажатием комбинации
CTRL+SHIFT+ENTER. 

LINEST /
ЛИНЕЙН

Дополняет функцию TREND и выводит некоторые
статистические значения, связанные с регрессией  

y=b+m₁x₁+…+m_J x_J+e

Синтаксис 

LINEST(known_y’s
)

Рис. 35 Таблица вывода функция LINEST

m_J, …,
m₂, m₁
и b – оценки регрессионных
коэффициентов;

s_J, …,
s₂, s₁
и s_b
– стандартные ошибки для оценок регрессионных коэффициентов;

R2 –
коэффициент детерминации;

s_y –
стандартная ошибка оценки y;

F – F-статистика;

DoF – число степеней
свободы;

SS_reg –
регрессионная сумма квадратов;

SS_res–
остаточная сумма квадратов.

Примечания 

• LINEST – это
  очень плохо сконструированная функция, очень неудобная в
  практическом применении;

• Примечания,
  представленные в описании функции полностью применимы к
  функции LINEST.

Пример 
 

Рис.36 Функция LINEST

Функция LINEST является функцией массива и ее ввод должен
завершаться нажатием комбинации CTRL+SHIFT+ENTER. 

3.6. Установка надстроек

Прежде чем  начать использовать надстройку, нужно
выполнить процедуру ее установки, которая состоит из двух частей.

В первой фазе файлы, входящие в пакет надстройки
размещают на компьютере. В некоторых пакетах имеется программа
Setup.exe, которая выполняет это автоматически. В других файлы нужно
размещать самостоятельно. Объясним, как это нужно сделать. В состав
пакета обязательно входит файл с расширением XLA и несколько
вспомогательных файлов с расширениями DLL, HLP и др. Все вспомогательные
файлы должны  размещаться в следующих директориях:
C:\Windows, или  C:\Windows\System или
C:\Windows\System32. Основной файл (с расширением XLA) может, в
принципе, находится в любом месте, но две директории являются
предпочтительными.

Microsoft рекомендует размещать файлы XLA в директории
C:\Documents and Settings\User\Application
Data\Microsoft\AddIns, где User – это
имя, под которым происходит вход в систему. Тогда этот файл можно быстро
загрузить на второй фазе установки. Однако, если рабочие книги
используются на нескольких компьютерах, с разными именами
User, то, при смене компьютера, связи с
основным файлом надстройки теряются и их приходится

обновлять.

Поэтому мы предлагаем поместить файл
Chemometrics.xla в директорию, которая имеет одно и то же имя на
разных компьютерах, например C:\Program
Files\Chemometrics. Автоматическая установка надстройки
Chemometrics Add-In
описана здесь.

Вторая фаза проводится из открытой книги Excel. В версии
2003 нужно выполнить последовательность команд
Tools-Add-Ins, а в версии 2007 последовательность:
Office Button-Excel Options-Add-Ins-Go. В
появившемся окне (см Рис. 45) нужно нажать Browse
и найти в компьютере нужный файл XLA.  

 

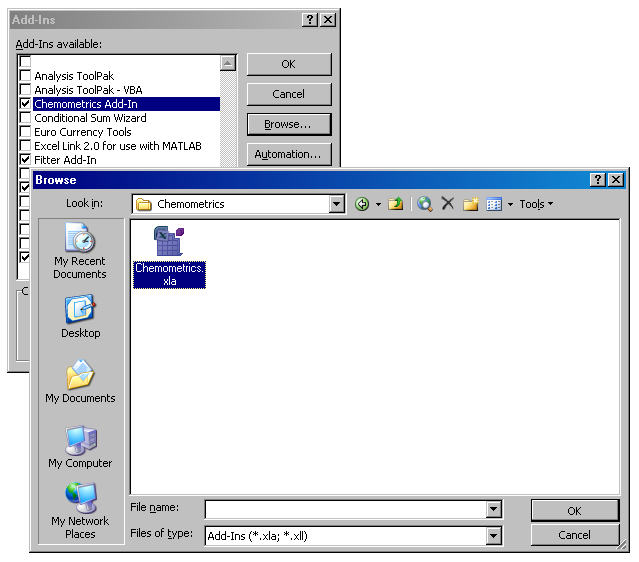
Рис.45 Установка надстройки

После того, как надстройка установлена, ее можно
активировать и деактивировать устанавливая отметку напротив имени. Для
удаления надстройки нужно снять галочку против ее имени в окне
Add-Ins, закрыть Excel и удалить все ранее
установленные файлы с компьютера.  

Заключение

Мы рассмотрели основные приемы работы с матрицами в
системе Excel

За рамками пособия осталось еще много всего важного. Частично заполнить эти пробелы поможет пособие Проекционные методы в
системе Excel

Как решить систему уравнений матричным методом в Excel

Дана система уравнений:

1. Значения элементов введем в ячейки Excel в виде таблицы.
2. Найдем обратную матрицу. Выделим диапазон, куда впоследствии будут помещены элементы матрицы (ориентируемся на количество строк и столбцов в исходной матрице). Открываем список функций (fx). В категории «Математические» находим МОБР. Аргумент – массив ячеек с элементами исходной матрицы.
3. Нажимаем ОК – в левом верхнем углу диапазона появляется значение. Последовательно жмем кнопку F2 и сочетание клавиш Ctrl + Shift + Enter.
4. Умножим обратную матрицу Ах-1х на матрицу В (именно в таком порядке следования множителей!). Выделяем диапазон, где впоследствии появятся элементы результирующей матрицы (ориентируемся на число строк и столбцов матрицы В). Открываем диалоговое окно математической функции МУМНОЖ. Первый диапазон – обратная матрица. Второй – матрица В.
5. Закрываем окно с аргументами функции нажатием кнопки ОК. Последовательно нажимаем кнопку F2 и комбинацию Ctrl + Shift + Enter.

Получены корни уравнений.

Как умножить столбец в Excel на число?

Для умножения столбца в Экселе на число можно составить формулу, указав в ней коэффициент умножения, а можно и без всяких формул через меню умножить весь выделенный диапазон значений на любое число.

Если число, на которое будут умножаться ячейки, находится в ячейке таблицы, то ссылку на эту ячейку в формуле нужно будет сделать абсолютной, чтобы она не менялась при применении формулы к другим ячейкам.

Также в Экселе есть возможность умножения диапазона значений на число с помощью специальной вставки с заменой исходных значений. Для этого нам понадобится скопировать наше число коэффициент в буфер обмена, выделить диапазон ячеек для умножения, и на вкладке «Главная»
в меню «Вставить»
выбрать «Специальная вставка…»
. Или такой же пункт выбрать в меню после нажатия на выделенный диапазон правой кнопкой мыши.

В появившемся окошке в графе «Операция»
выбираем «Умножить»
.

В дальнейшем число коэффициент поменять уже нельзя и все значения останутся неизменными.

В Экселе имеется функция ПРОИЗВЕД
, которая производит перемножение всех указанных в ней аргументов. Обязательный параметр только первый, в котором можно указать диапазон ячеек. Также можно выборочно перечислять ячейки через разделитель точка с запятой.

Как умножать в «Экселе» ячейки между собой?

В наши дни одним из самых популярных средств для сложных вычислений является программа Microsoft Excel. Её широкий функционал позволяет упростить решение множества задач, на которые раньше приходилось тратить немало времени. Сегодня мы рассмотрим, как умножать в «Экселе» ячейки между собой в больших количествах.

Прежде чем разобраться, как умножать в «Экселе» числа, стоит отметить широкую функциональность программы, позволяющей работать как с явным заданием чисел, так и с использованием ячеек, содержащих в себе и сами числа, и формулы, их определяющие. Для того чтобы умножить одну или несколько ячеек на число или другие ячейки, необходимо в строке формул после знака равенства указать данные элементы листа или записать значение самостоятельно.

Далее стоит уяснить принцип, как в «Экселе» умножить ячейку на ячейку и с какими проблемами можно встретиться в процессе. Для перемножения значений двух ячеек необходимо в строке формул прописать следующую конструкцию: «=А*В», где «А» и «В» — ссылки на соответствующие элементы листа «Экселя», то есть ячейки.

Получив результат, может потребоваться создание его копии, и нередко пользователи, не задумываясь, просто копируют значение этой ячейки, вставляя его в другую. Однако при таком подходе произойдёт изменение и соответствующих ссылок, указывавших на множители. Для того чтобы избежать такой ошибки, следует либо в ячейке, куда необходимо скопировать результат, ввести ссылку на копируемую ячейку, либо «зафиксировать» адрес её множителей с помощью знака «$». Знак доллара сохраняет значение ссылки по параметру, следующему за ним — то есть ссылка $A4 будет всегда относиться к столбцу А, A$4 — к четвертой строке, а $A$4 — только к ячейке А4. Другими словами, фиксация ячейки — создание абсолютной ссылки на неё.

Пользуясь алгоритмом закрепления адреса ячейки, можно перейти непосредственно к тому, как умножить в «Экселе» столбец на столбец или строку на строку. Чтобы не терять время на написание громадной формулы, можно просто воспользоваться свойством изменения ссылки на ячейку при переносе на новый адрес указателя. То есть, если необходимо перемножить попарно значения в двух столбцах, достаточно записать формулу умножения для первой пары ячеек, после чего, удерживая знак «чёрный плюс», появившийся в правом нижнем углу, растянуть результат вниз, вдоль всех значений столбцов-множителей.

Для того чтобы добиться аналогичного результата для строк, необходимо лишь произвести растягивание результата вдоль соответствующих строк. Стоит отметить: для того чтобы избежать сдвига при дальнейшем копировании результатов, нужно в формуле закрепить указанный столбец или строку — тогда удастся избежать ошибок при вычислении.