Округление чисел

Применение функций

Если же вы хотите изменить величину округления при расчете относительно одной или нескольких ячеек, но не хотите понижать точность расчетов в целом для документа, то в этом случае, лучше всего воспользоваться возможностями, которые предоставляет функция «ОКРУГЛ», и различные её вариации, а также некоторые другие функции.

Среди основных функций, которые регулируют округление, следует выделить такие:

• ОКРУГЛ – округляет до указанного числа десятичных знаков, согласно общепринятым правилам округления;
• ОКРУГЛВВЕРХ – округляет до ближайшего числа вверх по модулю;
• ОКРУГЛВНИЗ – округляет до ближайшего числа вниз по модулю;
• ОКРУГЛТ – округляет число с заданной точностью;
• ОКРВВЕРХ – округляет число с заданной точность вверх по модулю;
• ОКРВНИЗ – округляет число вниз по модулю с заданной точностью;
• ОТБР – округляет данные до целого числа;
• ЧЕТН – округляет данные до ближайшего четного числа;
• НЕЧЕТН – округляет данные до ближайшего нечетного числа.

Для функций ОКРУГЛ, ОКРУГЛВВЕРХ и ОКРУГЛВНИЗ следующий формат ввода: «Наименование функции (число;число_разрядов). То есть, если вы, например, хотите округлить число 2,56896 до трех разрядов, то применяете функцию ОКРУГЛ(2,56896;3). На выходе получается число 2,569.

Для функций ОКРУГЛТ, ОКРВВЕРХ и ОКРВНИЗ применяется такая формула округления: «Наименование функции(число;точность)». Например, чтобы округлить число 11 до ближайшего числа кратного 2, вводим функцию ОКРУГЛТ(11;2). На выходе получается число 12.

Функции ОТБР, ЧЕТН и НЕЧЕТ используют следующий формат: «Наименование функции(число)». Для того, чтобы округлить число 17 до ближайшего четного применяем функцию ЧЕТН(17). Получаем число 18.

Функцию можно вводить, как в ячейку, так и в строку функций, предварительно выделив ту ячейку, в которой она будет находиться. Перед каждой функцией нужно ставить знак «=».

Существует и несколько другой способ введения функций округления. Его особенно удобно использовать, когда есть таблица со значениями, которые нужно преобразовать в округленные числа в отдельном столбике.

Для этого, переходим во вкладку «Формулы». Кликаем по копке «Математические». Далее, в открывшемся списке выбираем нужную функцию, например ОКРУГЛ.

После этого, открывается окно аргументов функции. В поле «Число» можно ввести число вручную, но если мы хотим автоматически округлить данные всей таблицы, тогда кликаем по кнопке справа от окна введения данных.

Окно аргументов функции сворачивается. Теперь нужно кликнуть по самой верхней ячейке столбца, данные которого мы собираемся округлить. После того, как значение занесено в окно, кликаем по кнопке справа от этого значения.

Опять открывается окно аргументов функции. В поле «Число разрядов» записываем разрядность, до которой нам нужно сокращать дроби. После этого, жмем на кнопку «OK».

Как видим, число округлилось. Для того, чтобы таким же образом округлить и все другие данные нужного столбца, наводим курсор на нижний правый угол ячейки с округленным значением, жмем на левую кнопку мыши, и протягиваем её вниз до конца таблицы.

После этого, все значения в нужном столбце будут округлены.

Как видим, существуют два основных способа округлить видимое отображение числа: с помощью кнопки на ленте, и путем изменения параметров формата ячеек. Кроме того, можно изменить и округление реально рассчитываемых данных. Это также можно сделать двумя способами: изменением настроек книги в целом, или путем применения специальных функций. Выбор конкретного способа зависит от того, собираетесь ли вы применять подобный вид округления для всех данных в файле, или только для определенного диапазона ячеек.

Мы рады, что смогли помочь Вам в решении проблемы.

Помогла ли вам эта статья?

Да Нет

Округляют числа в Excel несколькими способами. С помощью формата ячеек и с помощью функций. Эти два способа следует различать так: первый только для отображения значений или вывода на печать, а второй способ еще и для вычислений и расчетов.

С помощью функций возможно точное округление, в большую или меньшую сторону, до заданного пользователем разряда. А полученные значения в результате вычислений, можно использовать в других формулах и функциях. В то же время округление с помощью формата ячеек не даст желаемого результата, и результаты вычислений с такими значениями будут ошибочны. Ведь формат ячеек, по сути, значение не меняет, меняется лишь его способ отображения. Чтобы в этом быстро и легко разобраться и не совершать ошибок, приведем несколько примеров.

Второе правило округления

Второе правило округления выглядит следующим образом:

Если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.

Например, округлим число 675 до разряда десятков.

В первую очередь находим сохраняемую цифру. Для этого надо прочитать само задание. В разряде, о котором говорится в задании и находится сохраняемая цифра. В задании сказано: округлить число 675 до разряда десятков.

Видим, что в разряде десятков находится семёрка. Значит сохраняемой цифрой является цифра 7

Теперь находим первую из отбрасываемых цифр. Первой из отбрасываемых цифр является та цифра, которая следует после сохраняемой цифрой. Видим, что первая цифра после семёрки это цифра 5. Значит цифра 5 является первой отбрасываемой цифрой.

Теперь применяем второе правило округления. Оно говорит, что если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.

У нас первая из отбрасываемых цифр это 5. Значит мы должны увеличить на единицу сохраняемую цифру 7, а всё что следует после неё заменить нулём:

675 ≈ 680

Значит при округлении числа 675 до разряда десятков, получаем приближённое ему число 680.

Теперь попробуем округлить то же самое число 675, но уже до разряда сотен.

Нам требуется округлить число 675 до разряда сотен. Снова ищем сохраняемую цифру. В этот раз сохраняемой цифрой является 6, поскольку мы округляем число до разряда сотен:

Теперь находим первую из отбрасываемых цифр. Первой из отбрасываемых цифр является та цифра, которая следует после сохраняемой цифрой. Видим, что первая цифра после шестёрки это цифра 7. Значит цифра 7 является первой отбрасываемой цифрой:

Теперь применяем второе правило округления. Оно говорит, что если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.

У нас первая из отбрасываемых цифр это 7. Значит мы должны увеличить на единицу сохраняемую цифру 6, а всё что следует после неё заменить нулями:

675 ≈ 700

Значит при округлении числа 675 до разряда сотен, получаем приближённое ему число 700.

Пример 3. Округлить число 9876 до разряда десятков.

Здесь сохраняемая цифра это 7. А первая отбрасываемая цифра это 6. Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.

Значит увеличиваем на единицу сохраняемую цифру 7, а всё что располагается после неё заменяем нулём:

9876 ≈ 9880

Пример 4. Округлить число 9876 до разряда сотен.

Здесь сохраняемая цифра это 8. А первая отбрасываемая цифра это 7. Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.

Значит увеличиваем на единицу сохраняемую цифру 8, а всё что располагается после неё заменяем нулями:

9876 ≈ 9900

Пример 5. Округлить число 9876 до разряда тысяч.

Здесь сохраняемая цифра это 9. А первая отбрасываемая цифра это 8. Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.

Значит увеличиваем на единицу сохраняемую цифру 9, а всё что располагается после неё заменяем нулями:

9876 ≈ 10000

Пример 6. Округлить число 2971 до сотен.

При округлении этого числа до сотен следует быть внимательным, поскольку сохраняемая цифра здесь 9, а первая отбрасываемая цифра это 7. Значит цифра 9 должна увеличиться на единицу. Но дело в том, что после увеличения девятки на единицу получится 10, а это цифра не вместится в разряд сотен нового числа.

В этом случае, в разряде сотен нового числа надо записать 0, а единицу перенести на следующий разряд и сложить с цифрой, которая там находится. Далее заменить все цифры после сохраняемой нулями:

2971 ≈ 3000

Тригонометрический калькулятор онлайн — примеры

Как произвести онлайн расчет синусов и косинусов, тангенсов

Обратите внимание, что kalkpro.ru способен оперировать как градусами, так радианами и градами. 1 рад = 57,3°; 360° = 2π рад., 1 град = 0,9 градусов или 1 град = 0,015708 радиан

1 рад = 57,3°; 360° = 2π рад., 1 град = 0,9 градусов или 1 град = 0,015708 радиан.

Для включения того или иного режима измерения нажмите нужную кнопку:

где Deg – градусы, Rad – измерение в радианах, Grad — в градах. По умолчанию включен режим расчета в градусах.

В качестве самого простого примера найдем синус 90 градусов. Нажмите:

90

Ответ: единица

Также рассчитываются и другие тригонометрические функции, например, вычислим косинус 60 °:

60

Решение: 0,5

Аналогичным способом вычисляются обратные тригонометрические функции онлайн на КАЛКПРО — арксинус , арккосинус, арктангенс, а также гиперболические функции sinh, cosh, tanh.

Для их ввода необходимо переключить интерфейс, нажав , появятся новые кнопки – asin, acos, atan. Порядок ввода данных прежний: сначала величину, затем символ нужной функции, будь то акрсинус или арккосинус.

Преобразование с кнопкой Dms и Deg на калькуляторе

позволяет перевести угол из формата градусы, минуты и секунды в десятичные доли градуса для вычислений. производит обратный перевод – в формат «градусы; минуты; секунды».

Например, угол 35 o 14 минут 04 секунды 53 десятые доли секунды переведем в десятые доли:

35,140453 35,23459166666666666666

Переведем в прежний формат: 35,23459166666666666666 35,140453

Десятичный логарифм онлайн

Десятичный логарифм на калькуляторе рассчитывается следующим образом, например, ищем log единицы по основанию 10, log10(1) или lg1:

1

Получается 0 в итоге. Для подсчета lg100 нажмем так:

100

Решение: два. Как себя проверить? Что вообще такое десятичный логарифм — log по основанию 10. В нашем примере 2 – это степень в которую необходимо ввести основание логарифма, то есть 10, чтобы получить 100.

Так же вычисляется натуральный логарифм, но кнопкой .

Как пользоваться памятью на калькуляторе

Существующие кнопки памяти: M+, M-, MR, MS, MC.

Добавить данные в память программы, чтобы потом провести с ними дальнейшие вычисления поможет операция MS.

MR выведет вам на дисплей сохраненную в памяти информацию. MC удалит любые данные из памяти. M- вычтет число на онлайн дисплее из запомненного в памяти.

Пример. Внесем сто сорок пять в память программы:

145

После проведения других вычислений нам внезапно понадобилось вернуть запомненное число на экран электронного калькулятора, нажимаем просто:

На экране отобразится снова 145.

Потом мы снова считаем, считаем, а затем решили сложить, к примеру, 85 с запомненным 145, для этого нажимаем , либо для вычитания 85 из запомненного 145. В первом случае по возвращению итогового числа из памяти кнопкой получится 230, а во втором, после нажатия и получится 60.

Инженерный калькулятор kalkpro.ru быстро и точно проведет сложные вычисления, значительно упрощая ваши задачи.

Перечень калькуляторов и функционал будет расширяться, просто добавьте сайт в закладки и расскажите друзьям!

Округление чисел

Для нахождения приближенного значения применяется такое действие как округление чисел.

Слово «округление» говорит само за себя. Округлить число значит сделать его круглым. Круглым называется число, которое оканчивается нулём. Например, следующие числа являются круглыми:

10, 20, 30, 100, 300, 700, 1000

Любое число можно сделать круглым. Процедуру, при которой число делают круглым, называют округлением числá.

Мы уже занимались «округлением» чисел, когда делили большие числа. Напомним, что для этого мы оставляли без изменения цифру, образующую старший разряд, а остальные цифры заменяли нулями. Но это были лишь наброски, которые мы делали для облегчения деления. Своего рода лайфхак. По факту, это даже не являлось округлением чисел. Именно поэтому в начале данного абзаца мы взяли слово округление в кавычки.

На самом деле, суть округления заключается в том, чтобы найти ближайшее значение от исходного. При этом, число может быть округлено до определённого разряда — до разряда десятков, разряда сотен, разряда тысяч.

Рассмотрим простой пример на округление. Дано число 17. Требуется округлить его до разряда десятков.

Не забегая вперёд попробуем понять, что означает «округлить до разряда десятков». Когда говорят округлить число 17, то надо понимать, что от нас требуют найти ближайшее круглое число от числá 17. Причём в ходе этого поиска возможно изменения коснутся и той цифры, которая располагается в разряде десятков числá 17 (т.е цифры 1).

Предстáвим числа от 10 до 20 с помощью следующего рисунка:

На рисунке видно, что для числá 17 ближайшее круглое число это число 20. Значит ответ к задаче таким и будет: «17 приближённо равно 20″

17 ≈ 20

Мы нашли приближённое значение для 17, то есть округлили его до разряда десятков. Видно, что после округления в разряде десятков появилась новая цифра 2.

Попробуем найти приближённое число для числа 12. Для этого снова предстáвим числа от 10 до 20 с помощью рисунка:

На рисунке видно, что ближайшее круглое число для 12 это число 10. Значит ответ к задаче таким и будет: 12 приближённо равно 10

12 ≈ 10

Мы нашли приближённое значение для 12, то есть округлили его до разряда десятков. В этот раз цифра 1, которая стояла в разряде десятков в числе 12, не пострадала от округления. Почему так получилось мы расскажем позже.

Попробуем найти ближайшее число для числá 15. Снова предстáвим числа от 10 до 20 с помощью рисунка:

На рисунке видно, что число 15 одинаково удалено от круглых чисел 10 и 20. Возникает вопрос: которое из этих круглых чисел будет приближённым значением для числа 15? Для таких случаев условились принимать бóльшее число за приближённое. 20 больше чем 10, поэтому приближённое значение для 15 будет число 20

15 ≈ 20

Округлять можно и большие числа. Естественно, для них делать рисунки и изображать числа не представляется возможным. Для них существует свой способ. Например, округлим число 1456 до разряда десятков.

Итак, мы должны округлить 1456 до разряда десятков. Разряд десятков начинается на пятёрке:

Теперь о существовании первых цифр 1 и 4 временно забываем. Остается число 56

Теперь смотрим, какое круглое число находится ближе к числу 56. Очевидно, что ближайшее круглое число для 56 это число 60. Значит заменяем число 56 на число 60

Значит при округлении числа 1456 до разряда десятков полýчим 1460

1456 ≈ 1460

Видно, что после округления числа 1456 до разряда десятков, изменения коснулись и самогó разряда десятков. В новом полученном числе в разряде десятков теперь располагается цифра 6, а не 5.

Округлять числа можно не только до разряда десятков. Округлять число можно до разряда сотен, тысяч, десятков тысяч и так далее.

После того, как станóвится ясно, что округление это ни что иное как поиск ближáйшего числá, можно применять готовые правила, которые значительно облегчают округление чисел.

Как пользоваться инженерным калькулятором – на примерах

Как возвести в степень

Чтобы возвести, к примеру, 12^3 вводите в следующей последовательности:

12 3

12, клавиша «икс в степени игрик» , 3, знак равенства

Ответ: 1728

Как найти корень кубический

Допустим, что мы извлекаем корень кубический из 729, нажмите в таком порядке:

729

729, «кубический корень из икс», равенства

Как найти корень на калькуляторе

Задача: Найти квадратный корень 36.

Решение: всё просто, нажимаем так:

36 y√x] 2

36, «корень из икса, в степени игрик», нужную нам степень 2, равно

Ответ: 6

При помощи этой функции вы можете найти корень в любой степени, не только квадратный.

Как возвести в квадрат

Для возведения в квадрат онлайн вычислительная программа содержит две функции:

«икс в степени игрик», «икс в квадрате»

Последовательность ввода данных такая же, как и раньше – сначала исходную величину, затем «x^2» и знак равно, либо если не квадрат, а произвольное число, необходимо нажать функцию «x^y», затем указать необходимую степень и так же нажать знак «равно».

Например: 45 6

Ответ: сорок пять в шестой степ. равно 8303765625

Округление десятичных дробей

Чтобы округлить десятичную дробь, нужно в записи числа выбрать разряд, до которого производится округление. Цифра, записанная в данном разряде:

• не меняется, если следующая за ней справа цифра — 0, 1, 2, 3 или 4;
• увеличивается на единицу, если следующая за ней справа цифра — 5,6,7,8 или 9.

Все цифры, стоящие справа от данного разряда, заменяются нулями. Если эти нули находятся в дробной части числа, то их не пишут.

Если в разряде, до которого производится округление, стоит цифра 9 и необходимо ее увеличить на единицу, то в этом разряде записывается цифра 0, а цифра в предыдущем разряде (слева) увеличивается на 1.

Округление чисел особенно часто требуется при денежных расчетах. Например, цену товара в рублях, как правило, нельзя устанавливать с точностью более двух знаков после запятой. Если же в результате вычислений получается большее число десятичных разрядов, требуется округление. В противном случае накапливание тысячных и десятитысячных долей рубля приведет в итоге к ошибкам в вычислениях.

Для округления чисел можно использовать целую группу функций.

Наиболее часто используют функции ОКРУГЛ, ОКРУГЛВВЕРХ и ОКРУГЛВНИЗ.

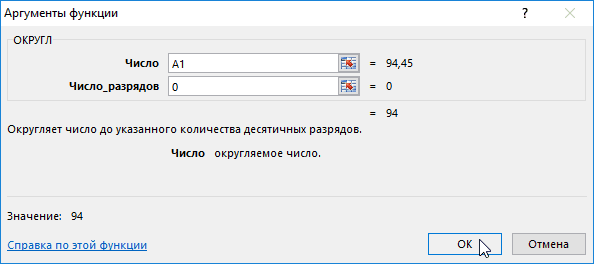
Синтаксис функции ОКРУГЛ

ОКРУГЛ(А;В),

где A – округляемое число;

Синтаксис функций ОКРУГЛВВЕРХ и ОКРУГЛВНИЗ точно такой же, что и у функции ОКРУГЛ.

Функция ОКРУГЛ при округлении отбрасывает цифры меньшие 5, а цифры большие 5 округляет до следующего разряда. Функция ОКРУГЛВВЕРХ при округлении любые цифры округляет до следующего разряда. Функция ОКРУГЛВНИЗ при округлении отбрасывает любые цифры. Пример округления до двух знаков после запятой с использованием функций ОКРУГЛ, ОКРУГЛВВЕРХ и ОКРУГЛВНИЗ приведен на рис. 7.4.

Рис. 7.4.
Округление до заданного количества десятичных разрядов

Функции ОКРУГЛ, ОКРУГЛВВЕРХ и ОКРУГЛВНИЗ можно использовать и для округления целых разрядов чисел. Для этого необходимо использовать отрицательные значения аргумента В.

Для округления чисел в меньшую сторону можно использовать также функцию ОТБР.

Синтаксис функции

ОТБР(А;В),

где A – округляемое число;

В – число знаков после запятой (десятичных разрядов), до которого округляется число.

Фактически функция ОТБР отбрасывает лишние знаки, оставляя только количество знаков, указанное в аргументе В.

Так же как и функции ОКРУГЛ, ОКРУГЛВВЕРХ и ОКРУГЛВНИЗ, функцию ОТБР можно использовать для округления целых разрядов чисел. Для этого необходимо использовать отрицательные значения аргумента В.

Для округления числа до меньшего целого можно использовать функцию ЦЕЛОЕ.

Синтаксис функции

где A – округляемое число.

Пример использования функции приведен на рис. 7.5.

Рис. 7.5.
Округление до целого числа

Для округления числа с заданной точностью можно использовать функцию ОКРУГЛТ.

Синтаксис функции

ОКРУГЛТ(А;В),

где A – округляемое число;

В – точность, с которой требуется округлить число.

Функция ОКРУГЛТ производит округление с избытком. Округление производится в том случае, если остаток от деления числа на точность больше или равен половине точности. Пример использования функции приведен на рис. 7.6.

Рис. 7.6.
Округления с заданной точностью

Наконец, для округления до ближайшего четного или нечетного числа можно использовать функции ЧЕТН и НЕЧЕТН, а для ближайшего кратного большего или меньшего числа – функции ОКРВЕРХ и ОКРВНИЗ.

Синтаксис функции ЧЕТН

где A – округляемое число.

Функция НЕЧЕТН имеет такой же синтаксис.

Обе функции округляют положительные числа до ближайшего большего четного или нечетного числа, а отрицательные – до ближайшего меньшего четного или нечетного числа.

Синтаксис функции ОКРВВЕРХ

ОКРВВЕРХ(А;В),

где A – округляемое число;

В – кратное, до которого требуется округлить.

Функция ОКРВНИЗ имеет такой же синтаксис.

Следует обратить внимание на различие в округлении и установке отображаемого числа знаков после запятой с использованием средств форматирования. При использовании числовых форматов изменяется только отображаемое число, а в вычислениях используется хранимое значение

Чтобы быстро сделать так, чтобы число казалось округленным, измените количество десятичных разрядов. Просто выделите число, которое вы хотите округлить, и щелкните Главная
> Уменьшить разрядность

.

Число в ячейке будет казаться округленным, но фактическое значение не изменится — при ссылке на ячейку будет использоваться полное значение.

ОКРУГЛТ

Довольно интересная функция ОКРУГЛТ. С ее помощью можно добиться округления не только до нужного разряда (слева или справа от запятой), но и вообще до нужной точности (кратности). К примеру, нужно рассчитать заказ изделий в штуках, но так, чтобы он был равен целому количеству ящиков. Если в ящике 6 шт, то заказываемое у поставщика количество должно быть кратным шести. Или другой пример. Нужно, чтобы расчетная цена заканчивалась либо на 00, либо на 50, то есть имела кратность 50 рублей. В обоих случаях функция ОКРУГЛТ решает задачу в одно действие.

Очень, очень правильная функция. Позволяет избежать 3-х промежуточных расчетов (разделить на кратность, округлить до целого и снова умножить на кратность, как я сам делал, пока не узнал про эту формулу).

Работа с файлами

Сочетание клавиш	Описание
Shift + F10Menu	Отображение контекстного меню текущего объекта (аналогично нажатию правой кнопкой мыши).
Alt + Enter	Вызов «Свойств объекта»
F2	Переименование объекта
Перетаскивание с Ctrl	Копирование объекта
Перетаскивание с Shift	Перемещение объекта
Перетаскивание с Ctrl + Shift	Создание ярлыка объекта
Щелчки с Ctrl	Выделение нескольких объектов в произвольном порядке
Щелчки с Shift	Выделение нескольких смежных объектов
Enter	То же, что и двойной щелчок по объекту
Delete	Удаление объекта
Shift + Delete	Безвозвратное удаление объекта, не помещая его в корзину

Как округлить число форматом ячейки

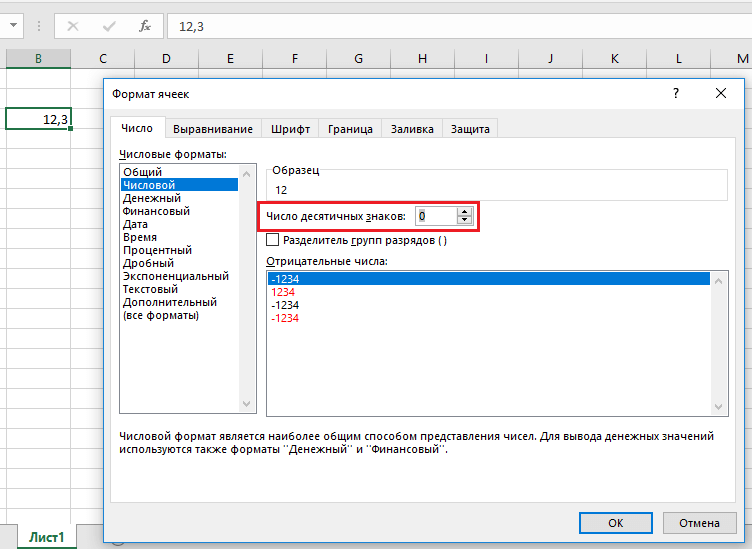
Впишем в ячейку А1 значение 76,575. Щелкнув правой кнопкой мыши, вызываем меню «Формат ячеек». Сделать то же самое можно через инструмент «Число» на главной странице Книги. Или нажать комбинацию горячих клавиш CTRL+1.

Выбираем числовой формат и устанавливаем количество десятичных знаков – 0.

Результат округления:

Назначить количество десятичных знаков можно в «денежном» формате, «финансовом», «процентном».

Как видно, округление происходит по математическим законам. Последняя цифра, которую нужно сохранить, увеличивается на единицу, если за ней следует цифра больше или равная «5».

Особенность данного варианта: чем больше цифр после запятой мы оставим, тем точнее получим результат.

Получение приближенных значений

Это математическое действие осуществляется по определенным правилам.

Но для каждого множества чисел они разные. Отмечают, что округлить можно целые числа и десятичные .

А вот с обыкновенными дробями действие не выполняется.

Сначала их необходимо перевести в десятичные дроби
, а затем приступить к процедуре в необходимом контексте.

Правила приближения значений заключаются в следующем:

• для целых – замена разрядов, следующих за округляемым, нулями;
• для десятичных дробей – отбрасывания всех чисел, которые находятся за округляемым разрядом.

К примеру, округляя 303 434 до тысяч, необходимо заменить сотни, десятки и единицы нулями, то есть 303 000. В десятичных дробях 3,3333 округляя до десяты
х, просто отбрасывают все последующие цифры и получают результат 3,3.

Округление при работе с числами ограниченной точности

Реальные физические величины всегда измеряются с некоторой конечной точностью, которая зависит от приборов и методов измерения и оценивается максимальным относительным или абсолютным отклонением неизвестного истинного значения от измеренного, что в десятичном представлении значения соответствует либо определённому числу значащих цифр, либо определённой позиции в записи числа, все цифры после (правее) которой являются незначащими (лежат в пределах погрешности измерения). Сами измеренные параметры записываются с таким числом знаков, чтобы все цифры были надёжными, возможно, последняя — сомнительной. Погрешность при математических операциях с числами ограниченной точности сохраняется и изменяется по известным математическим законам, поэтому когда в дальнейших вычислениях возникают промежуточные значения и результаты с больши́м числом цифр, из этих цифр только часть являются значимыми. Остальные цифры, присутствуя в значениях, фактически не отражают никакой физической реальности и лишь отнимают время на вычисления. Вследствие этого промежуточные значения и результаты при вычислениях с ограниченной точностью округляют до того количества знаков, которое отражает реальную точность полученных значений. На практике обычно рекомендуется при длинных «цепочных» ручных вычислениях сохранять в промежуточных значениях на одну цифру больше. При использовании компьютера промежуточные округления в научно-технических приложениях чаще всего теряют смысл, и округляется только результат.

Так, например, если задана сила 5815 гс с точностью до грамма силы и длина плеча 1,40 м с точностью до сантиметра, то момент силы в кгс по формуле M=(mg)⋅h{\displaystyle M=(mg)\cdot h}, в случае формального расчёта со всеми знаками, окажется равным: 5,815 кгс • 1,4 м = 8,141 кгс•м. Однако если учесть погрешность измерения, то мы получим, что предельная относительная погрешность первого значения составляет 1/5815 ≈ 1,7•10−4, второго — 1/140 ≈ 7,1•10−3, относительная погрешность результата по правилу погрешности операции умножения (при умножении приближённых величин относительные погрешности складываются) составит 7,3•10−3, что соответствует максимальной абсолютной погрешности результата ±0,059 кгс•м! То есть в реальности, с учётом погрешности, результат может составлять от 8,082 до 8,200 кгс•м, таким образом, в рассчитанном значении 8,141 кгс•м полностью надёжной является только первая цифра, даже вторая — уже сомнительна! Корректным будет округление результата вычислений до первой сомнительной цифры, то есть до десятых: 8,1 кгс•м, или, при необходимости более точного указания рамок погрешности, представить его в виде, округлённом до одного-двух знаков после запятой с указанием погрешности: 8,14 ± 0,06 кгс•м.

Округление рассчитанного значения погрешности

Обычно в окончательном значении рассчитанной погрешности оставляют только первые одну-две значащие цифры. По одному из применяемых правил, если значение погрешности начинается с цифр 1 или 2(по другому правилу — 1, 2 или 3), то в нём сохраняют две значащих цифры, в остальных случаях — одну, например: 0,13; 0,26; 0,3; 0,8. То есть каждая декада возможных значений округляемой погрешности разделена на две части. Недостаток этого правила состоит в том, что относительная погрешность округления изменяется значительным скачком при переходе от числа 0,29 к числу 0,3. Для устранения этого предлагается каждую декаду возможных значений погрешности делить на три части с менее резким изменением шага округления. Тогда ряд разрешённых к употреблению округлённых значений погрешности получает вид:

• 0,10; 0,12; 0,14; 0,16; 0,18;
• 0,20; 0,25; 0,30; 0,35; 0,40; 0,45;
• 0,5; 0,6; 0,7; 0,8; 0,9; 1,0.

Однако при использовании такого правила последние цифры самого результата, оставляемые после округления, также должны соответствовать приведённому ряду.

Пересчёт значений физических величин

Пересчёт значения физической величины из одной системы единиц в другую должен производиться с сохранением точности исходного значения. Для этого исходное значение в одних единицах следует умножить (разделить) на переводной коэффициент, часто содержащий большое количество значащих цифр, и округлить полученный результат до количества значащих цифр, обеспечивающего точность исходного значения. Например, при пересчёте значения силы 96,3 тс в значение, выраженное в килоньютонах (кН), следует умножить исходное значение на переводной коэффициент 9,80665 (1 тс = 9,80665 кН). В результате получается значение 944,380395 кН, которое необходимо округлить до трёх значащих цифр. Вместо 96,3 тс получаем 944 кН.