Функция агрегат (aggregate)

Нахождение обратной матрицы с помощью элементарных преобразований (метод Гаусса)

Пример 3. Методом элементарных преобразований вычислить -1 если = .

Решение. Приписываем к исходной справа единичную того же порядка: . С помощью элементарных преобразований столбцов приведём левую “половину” к единичной, совершая одновременно точно такие преобразования над правой «половиной».
Поменяем местами 1 со 2 столбцы: ~. К третьему прибавим первый, ко второму — первый, × на -2: . Из первого вычтем удвоенный второй, из третьего — × на 6 второй; . Прибавим третий к первому и второму: . Умножим последний на минус один: . Справа от вертикальной черты квадратная таблица размером 3х3 .

Восстановление удаленного видео

Для восстановления удаленного видео мы изучим три совершенно разных способа, в которых будет пошагово рассмотрено как выполнить те или иные действия. Следуйте представленным инструкциям для достижения максимального результата.

Справочная поддержка

Отправьте письмо в службу поддержки, чтобы восстановить утерянные или стертые видео YouTube с вашего канала. Кроме того, ваш канал должен иметь не менее 10 000 просмотров или участвовать в партнерской программе YouTube. Выполните следующие действия, чтобы связаться со службой поддержки:

1. Войдите в свой канал, прокрутите вниз до нижней части страницы и нажмите «Справка».
2. Нажмите – Нужна дополнительная помощь
3. В категории выберите нужную проблему и нажмите «Поддержка по электронной почте».
4. Кроме того, вам также может понадобиться нажать ссылку «Связаться со службой поддержки».

Выполните краткую пошаговую инструкцию для связи со службой поддержки и заполнения формы для восстановления:

1. Заходим на сайт YouTube.
2. В левом меню кликаем на пункт – Мой канал.
3. Выбираем Менеджер видео.
4. Теперь в левой колонке в самом низу нажимаем на черную кнопку – Справка и отзывы.
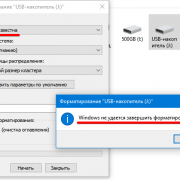
5. Появится узкое всплывающее окно, в котором выбираем вид связи – Электронная почта.
6. Затем под заголовком – Чем мы можем вам помочь, выберите – Правила и принципы сообщества.
7. Заполните представленную форму на изображении.

Затем вы можете попробовать скачать видео и использовать его снова. Если этот метод не помогает, воспользуйтесь следующим способом, пока ожидаете ответа от службы поддержки.

Восстановление удаленных оригинальных видеофайлов на ПК

Этот метод поможет блогерам надежно восстановить утерянные видеофайлы на своём компьютере. Мощное программное обеспечение для восстановления видео – EaseUS Data Recovery Wizard эффективно поможет вам найти потерянные оригинальные видеофайлы YouTube за 3 простых шага в Windows 10/8/7:

Шаг 1 – Запустите программное обеспечение для восстановления видео

Запустите EaseUS Data Recovery Wizard и выберите место или устройство, где вы удалили видео. Нажмите кнопку “Сканировать”, чтобы отсканировать и найти отсутствующие видео.

Шаг 2 – Найти удаленные видео

После проверки просмотрите свои удаленные видео на вкладке Удаленные файлы. Дважды щелкните по идентифицированным видео и просмотрите их в появившемся окне.

Шаг 3 – Выбирай и восстанавливай

Выберите видеофайлы, которые вы хотите восстановить. Нажмите кнопку “Восстановить”, чтобы сохранить найденные видео в безопасном месте на вашем ПК или другом безопасном внешнем устройстве хранения.

Нахождение обратной матрицы методом алгебраических дополнений (союзной матрицы)

Для неособенной квадратной матрицы А обратной является матрица

,  (2)

где —
определитель матрицы А, а

— матрица, союзная с матрицей А.

Разберём ключевые понятия, которые потребуются для решения задач — союзная матрица, алгебраические дополнения и транспонированная матрица.

Пусть существует квадратная матрица A:

Транспонированная относительно матрицы A матрица A’ получается,
если из строк матрицы A сделать столбцы, а из её столбцов — наоборот, строки, то есть заменить строки
столбцами:

Остановимся на минорах и алгебраических дополнениях.

Пусть есть квадратная матрица третьего порядка:

.

Её определитель:

Вычислим алгебраическое дополнение элемента ,
то есть элемента 2, стоящего на пересечении первой строки и второго столбца.

Для этого нужно сначала найти минор этого элемента. Он получается вычёркиванием из
определителя строки и столбца, на пересечении которых стоит указанный элемент. В результате останется
следующий определитель, который и является минором элемента :

.

Алгебраическое дополнение элемента
получим, если умножим ,
где i — номер строки исходного элемента, а k — номер столбца исходного элемента, на
полученный в предыдущем действии минор этого исходного элемента. Получаем алгебраическое дополнение элемента
:

.

По этой инструкции нужно вычислить алгебраические дополнения всех элементов матрицы
A’, транспонированной относительно матрицы матрица A.

И последнее из значимых для нахождение обратной матрицы понятий. Союзной с квадратной матрицей A называется матрица

того же порядка, элементами которой являются алгебраические дополнения соответствующих элементов определителя матрицы
,
транспонированной относительно матрицы A. Таким образом, союзная матрица состоит из следующих элементов:

Алгоритм нахождения обратной матрицы методом алгебраических дополнений

1. Найти определитель данной матрицы A. Если определитель равен нулю, нахождение
обратной матрицы прекращается, так как матрица вырожденная и обратная для неё не существует.

2. Найти матрицу, транспонированную относительно A.

3. Вычислить элементы союзной матрицы как алгебраические дополнения марицы, найденной на шаге 2.

4. Применить формулу (2): умножить число, обратное определителю матрицы A,
на союзную матрицу, найденную на шаге 4.

5. Проверить полученный на шаге 4 результат, умножив данную матрицу A на
обратную матрицу. Если произведение этих матриц равно единичной матрицы, значит обратная матрица была
найдена верно. В противном случае начать процесс решения снова.

Пример 1. Для матрицы

найти обратную матрицу.

Решение. Для нахождения обратной матрицы необходимо найти определитель матрицы А .
Находим по правилу треугольников:

Следовательно, матрица А – неособенная (невырожденная, несингулярная) и для неё существует обратная.

Найдём матрицу, союзную с данной матрицей А.

Найдём матрицу
,
транспонированную относительно матрицы A:

Вычисляем элементы союзной матрицы как алгебраические дополнения матрицы,
транспонированной относительно матрицы A:

Следовательно, матрица
,
союзная с матрицей A, имеет вид

Замечание. Порядок вычисления элементов и транспонирования матрицы может
быть иным. Можно сначала вычислить алгебраические дополнения матрицы A, а затем транспонировать
матрицу алгебраических дополнений. В результате должны получиться те же элементы союзной матрицы.

Применяя формулу (2), находим матрицу, обратную матрице А:

Проверить решение можно с помощью онлайн калькулятора
для нахождения обратной матрицы.

Решение систем уравнений методом Гаусса в Excel

Для примера возьмем простейшую систему уравнений:

3а + 2в – 5с = -12а – в – 3с = 13а + 2в – с = 9

Коэффициенты запишем в матрицу А. Свободные члены – в матрицу В.

Для наглядности свободные члены выделим заливкой. Если в первой ячейке матрицы А оказался 0, нужно поменять местами строки, чтобы здесь оказалось отличное от 0 значение.

1. Приведем все коэффициенты при а к 0. Кроме первого уравнения. Скопируем значения в первой строке двух матриц в ячейки В6:Е6. В ячейку В7 введем формулу: =B3:Е3-$B$2:$Е$2*(B3/$B$2). Выделим диапазон В7:Е7. Нажмем F2 и сочетание клавиш Ctrl + Shift + Enter. Мы отняли от второй строки первую, умноженную на отношение первых элементов второго и первого уравнения.
2. Копируем введенную формулу на 8 и 9 строки. Так мы избавились от коэффициентов перед а. Сохранили только первое уравнение.
3. Приведем к 0 коэффициенты перед в в третьем и четвертом уравнении. Копируем строки 6 и 7 (только значения). Переносим их ниже, в строки 10 и 11. Эти данные должны остаться неизменными. В ячейку В12 вводим формулу массива.
4. Прямую прогонку по методу Гаусса сделали. В обратном порядке начнем прогонять с последней строки полученной матрицы. Все элементы данной строки нужно разделить на коэффициент при с. Введем в строку формулу массива: <=B12:E12/D12>.
5. В строке 15: отнимем от второй строки третью, умноженную на коэффициент при с второй строки (<=(B11:E11-B16:E16*D11)/C11>). В строке 14: от первой строки отнимаем вторую и третью, умноженные на соответствующие коэффициенты (<=(B10:E10-B15:E15*C10-B16:E16*D10)/B10>). В последнем столбце новой матрицы получаем корни уравнения.

Анализ данных с помощью формулы массива

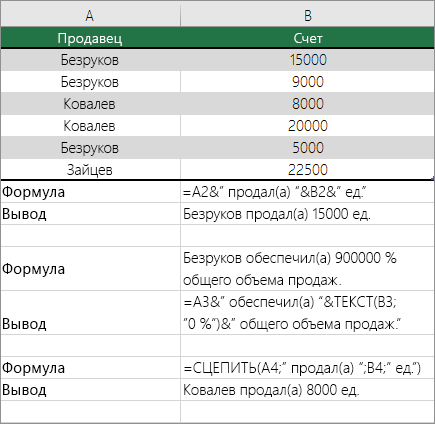
Формулы массива очень удобно использовать, если стоит задача анализировать информацию. В частности, можно проверять ее на предмет соответствия определенному критерию. Допустим, у нас есть такая таблица, в которой описываются продажи разными менеджерами. В одном отделе работает три сотрудника, а также продается три вида товаров. Ну и наконец, каждый из них имеет свою цену, а итоговая стоимость записывается в третьей колонке таблицы.

17

Перед нами стоит задача определить, насколько каждый из менеджеров является эффективным, учитывая продаваемые ими товары. Это можно сделать и самостоятельно, но с помощью формулы массива данную задачу можно выполнить буквально в несколько кликов. 

Давайте запишем в подходящих ячейках информацию, которая будет служить критерием для оценки эффективности. В нашем случае это товар и идентификатор менеджера, которого мы проверяем.

18

Чтобы успешно решить эту задачу, достаточно просто воспользоваться небольшой формулой массива.

Конечная наша цель – получение суммы, поэтому нужно использовать соответствующую функцию. Кроме этого, нам надо применить условие, на соответствие которым будет проверяться диапазон.

В результате получится формула, приведенная на скриншоте.

19

В ней используется 3 множителя. Первый проверяет менеджеров. Второй – товары. А третий – непосредственно определяет сумму заказа.

Как работает эта формула? Да очень просто. Ее алгоритм следующий:

1. Сначала Excel проверяет всех менеджеров и товары, соответствуют ли они заданным критериям. Если да, функция возвращает значение 1, если нет – 0.

2. В случае несоответствия значений хотя бы одному из условий, один из множителей становится равным нулю. Соответственно, и итоговый результат будет аналогичным.
3. Если же оба условия выполняются, то функция осуществляет операцию умножения.
4. Наконец, все полученные значения суммируются, после чего ячейка выдает общую эффективность по обработанным заказам. 

Вот таким образом можно простую формулу использовать, чтобы выполнять даже самую сложную обработку информации. В конечном итоге, можно несколько модернизировать отчет, добавив выпадающий список, в котором выбираются товары и менеджеры. Но это уже совсем другая тема.

3 .6. Установка надстроек

Прежде чем начать использовать надстройку, нужно
выполнить процедуру ее установки
, которая состоит из двух частей.

В первой фазе файлы, входящие в пакет надстройки
размещают на компьютере. В некоторых пакетах имеется программа
Setup.exe, которая выполняет это автоматически. В других файлы нужно
размещать самостоятельно. Объясним, как это нужно сделать. В состав
пакета обязательно входит файл с расширением XLA и несколько
вспомогательных файлов с расширениями DLL, HLP и др. Все вспомогательные
файлы должны размещаться в следующих директориях:
C:\Windows
, или C:\Windows\System или
C:\Windows\System32
. Основной файл (с расширением XLA) может, в
принципе, находится в любом месте, но две директории являются
предпочтительными.

Microsoft рекомендует размещать файлы XLA в директории
C:\Documents and Settings\User\Application
Data\Microsoft\AddIns
, где User
– это
имя, под которым происходит вход в систему. Тогда этот файл можно быстро
загрузить на второй фазе установки. Однако, если рабочие книги
используются на нескольких компьютерах, с разными именами
User
, то, при смене компьютера, связи с
основным файлом надстройки теряются и их приходится
обновлять .

Поэтому мы предлагаем поместить файл
Chemometrics.xla
в директорию, которая имеет одно и то же имя на
разных компьютерах, например C:\Program
Files\Chemometrics
. Автоматическая установка надстройки
Chemometrics Add-In

описана .

Вторая фаза проводится из открытой книги Excel. В версии
2003 нужно выполнить последовательность команд
Tools-Add-Ins
, а в версии 2007 последовательность:
Office Button-Excel Options-Add-Ins-Go
. В
появившемся окне (см Рис. 45
) нужно нажать Browse
и найти в компьютере нужный файл XLA.

Рис.45
Установка надстройки

После того, как надстройка установлена, ее можно
активировать и деактивировать устанавливая отметку напротив имени. Для
удаления надстройки нужно снять галочку против ее имени в окне
Add-Ins
, закрыть Excel и удалить все ранее
установленные файлы с компьютера.

Заключение

Мы рассмотрели основные приемы работы с матрицами в
системе Excel

За рамками пособия осталось еще много всего важного.
Частично заполнить эти пробелы поможет пособие. В программе Excel с матрицей можно работать как с диапазоном

То есть совокупностью смежных ячеек, занимающих прямоугольную область

В программе Excel с матрицей можно работать как с диапазоном. То есть совокупностью смежных ячеек, занимающих прямоугольную область.

Адрес матрицы – левая верхняя и правая нижняя ячейка диапазона, указанные черед двоеточие.

1.2. Книга, лист и ячейка

Файл Excel с расширением XLS (XLSX в версии 2007) называется
(рабочей) книгой. Если запустить программу Excel, например, щелкнуть на
рабочем столе иконку
,
то откроется новая пустая книга. . 

Рис. 2 Новая книга Excel

Если рабочая книга уже существует, то ее проще открыть через проводник. Для
этого достаточно щелкнуть по иконке файла.  

Рис. 3
Открытие книги Excel через проводник

Рабочая книга состоит из нескольких листов, имена которых
показаны в нижней части окна. Листы можно удалять, добавлять,
переименовывать. Для этого надо щелкнуть правой клавишей мышки по имени
листа. Появится меню, из которого можно выбрать нужную операцию.

Рис.
4 Операции с листами

Стандартное имя листа – Sheet1, но ему можно дать любое имя, например
Data. На лист можно вставлять рисунки, графики и другие необходимые
объекты.

Каждый лист состоит из ячеек, образующих таблицу, размером 256
столбцов и 65536 строк (В версии 2007 – 16384 столбцов и1048576 строк).
Строки на листе обозначены числами: 1,2, 3…, а столбцы имеют буквенную
кодировку: A, B, …,Z,
AA, AB .., и т.д. до последнего столбца
IV (в 2007
– до XFD). Этот стиль адресации называется A1. Реже применяется
альтернативный стиль R1C1, в котором столбцы также нумеруются. Мы не
будем использовать этот стиль, а прочитать об этом можно

здесь

Строки и столбцы можно удалять, добавлять, прятать, а также менять их размер:
высоту или ширину.

Все операции на листе выполняются с помощью меню, представленного в
верхней части окна (). Меню в Excel 2007
существенно отличается от прежней версии. Там, вместо обычных иконок,
появилась лента. Мы не будем подробно разбирать отличия версий. Те, кому
это интересно могут прочитать

здесь.

Решение уравнений методом подбора параметров Excel

Инструмент «Подбор параметра» применяется в ситуации, когда известен результат, но неизвестны аргументы. Excel подбирает значения до тех пор, пока вычисление не даст нужный итог.

Путь к команде: «Данные» — «Работа с данными» — «Анализ «что-если»» — «Подбор параметра».

Рассмотрим на примере решение квадратного уравнения х 2 + 3х + 2 = 0. Порядок нахождения корня средствами Excel:

1. Введем в ячейку В2 формулу для нахождения значения функции. В качестве аргумента применим ссылку на ячейку В1.
2. Открываем меню инструмента «Подбор параметра». В графе «Установить в ячейку» — ссылка на ячейку В2, где находится формула. В поле «Значение» вводим 0. Это то значение, которое нужно получить. В графе «Изменяя значение ячейки» — В1. Здесь должен отобразиться отобранный параметр.
3. После нажатия ОК отобразится результат подбора. Если нужно его сохранить, вновь нажимаем ОК. В противном случае – «Отмена».

Для подбора параметра программа использует циклический процесс. Чтобы изменить число итераций и погрешность, нужно зайти в параметры Excel. На вкладке «Формулы» установить предельное количество итераций, относительную погрешность. Поставить галочку «включить итеративные вычисления».

Формулы массива

В подавляющем количестве задач при работе с массивами (а матрицы и являются таковыми) используются формулы соответствующего типа. Базовое их отличие от обычных заключается в том, что последние выводят всего одно значение. Для применения формулы массива необходимо осуществить несколько действий:

1. Выделить набор ячеек, где будут выводиться значения. 
2. Непосредственно введение формулы. 
3. Нажатие последовательности клавиш Ctrl + Shift + Ввод.

После осуществления этих простых действий в поле ввода отображается формула массива. Ее можно отличить от обычной по фигурным скобкам.

Для редактирования, удаления формул массива, надо выделить требуемый диапазон и сделать то, что нужно. Чтобы редактировать матрицу, нужно использовать ту же комбинацию, что и для ее создания. При этом нет возможности редактировать отдельный элемент массива.

Транспонирование

Транспонировать матрицу – поменять строки и столбцы местами.

Сначала отметим пустой диапазон, куда будем транспонировать матрицу. В исходной матрице 4 строки – в диапазоне для транспонирования должно быть 4 столбца. 5 колонок – это пять строк в пустой области.

1 способ. Выделить исходную матрицу. Нажать «копировать». Выделить пустой диапазон. «Развернуть» клавишу «Вставить». Открыть меню «Специальной вставки». Отметить операцию «Транспонировать». Закрыть диалоговое окно нажатием кнопки ОК.

2 способ. Выделить ячейку в левом верхнем углу пустого диапазона. Вызвать «Мастер функций». Функция ТРАНСП. Аргумент – диапазон с исходной матрицей.

Нажимаем ОК. Пока функция выдает ошибку. Выделяем весь диапазон, куда нужно транспонировать матрицу. Нажимаем кнопку F2 (переходим в режим редактирования формулы). Нажимаем сочетание клавиш Ctrl + Shift + Enter.

Преимущество второго способа: при внесении изменений в исходную матрицу автоматически меняется транспонированная матрица.

Сложение

Складывать можно матрицы с одинаковым количеством элементов. Число строк и столбцов первого диапазона должно равняться числу строк и столбцов второго диапазона.

В первой ячейке результирующей матрицы нужно ввести формулу вида: = первый элемент первой матрицы + первый элемент второй: (=B2+H2). Нажать Enter и растянуть формулу на весь диапазон.

Умножение матриц в Excel

Условие задачи:

Чтобы умножить матрицу на число, нужно каждый ее элемент умножить на это число. Формула в Excel: =A1*$E$3 (ссылка на ячейку с числом должна быть абсолютной).

Умножим матрицу на матрицу разных диапазонов. Найти произведение матриц можно только в том случае, если число столбцов первой матрицы равняется числу строк второй.

В результирующей матрице количество строк равняется числу строк первой матрицы, а количество колонок – числу столбцов второй.

Для удобства выделяем диапазон, куда будут помещены результаты умножения. Делаем активной первую ячейку результирующего поля. Вводим формулу: =МУМНОЖ(A9:C13;E9:H11). Вводим как формулу массива.

Обратная матрица в Excel

Ее имеет смысл находить, если мы имеем дело с квадратной матрицей (количество строк и столбцов одинаковое).

Размерность обратной матрицы соответствует размеру исходной. Функция Excel – МОБР.

Выделяем первую ячейку пока пустого диапазона для обратной матрицы. Вводим формулу «=МОБР(A1:D4)» как функцию массива. Единственный аргумент – диапазон с исходной матрицей. Мы получили обратную матрицу в Excel:

Нахождение определителя матрицы

Это одно единственное число, которое находится для квадратной матрицы. Используемая функция – МОПРЕД.

Ставим курсор в любой ячейке открытого листа. Вводим формулу: =МОПРЕД(A1:D4).

Таким образом, мы произвели действия с матрицами с помощью встроенных возможностей Excel.

Что можно делать с матрицами

В целом, есть огромное количество действий, применение которых возможно для матриц. Давайте каждое из них рассмотрим более подробно.

Транспонирование

Многие люди не понимают значения этого термина. Представьте, что вам нужно поменять строки и колонки местами. Вот это действие и называется транспонированием. 

Перед тем, как это осуществить, необходимо выделить отдельную область, которая имеет такое же количество строчек, сколько столбцов есть у исходной матрицы и такое же количество столбцов. Чтобы более наглядно понять, как это работает, посмотрите на этот скриншот.

Далее есть несколько методов, как можно осуществить транспонирование. 

Первый способ следующий. Для начала нужно выделить матрицу, после чего скопировать ее. Далее выделяется диапазон ячеек, куда должен быть вставлен транспонированный диапазон. Далее открывается окно «Специальная вставка».

Там есть множество операций, но нам нужно найти радиокнопку «Транспонировать». После совершения этого действия нужно подтвердить его нажатием клавиши ОК.

Есть еще один способ, с помощью которого можно транспонировать матрицу. Сперва надо выделить ячейку, расположенную в верхнем левом углу диапазона, отведенного под транспонированную матрицу. Далее открывается диалоговое окно с функциями, где есть функция ТРАНСП. Ниже в примере вы более подробно узнаете, как это сделать. В качестве параметра функции используется диапазон, соответствующий изначальной матрице.

После нажатия кнопки ОК сначала будет показано, что вы допустили ошибку. Ничего в этом страшного нет. Все потому, что вставленная нами функция не определена, как формула массива. Поэтому нам нужно совершить такие действия:

1. Выделить набор ячеек, отведенных под транспонированную матрицу.
2. Нажать клавишу F2.
3. Нажать на горячие клавиши Ctrl + Shift + Enter.

Главное достоинство метода заключается в способности транспонированной матрицы сразу корректировать содержащуюся в ней информацию, как только вносятся данные в изначальную. Поэтому рекомендуется использовать именно данный способ.

По данным портала ЗАЧЕСТНЫЙБИЗНЕСМУНИЦИПАЛЬНОЕ КАЗЕННОЕ УЧРЕЖДЕНИЕ «УПРАВЛЕНИЕ КАПИТАЛЬНОГО СТРОИТЕЛЬСТВА МУНИЦИПАЛЬНОГО ОБРАЗОВАНИЯ БРЮХОВЕЦКИЙ РАЙОН»По данным портала ЗАЧЕСТНЫЙБИЗНЕС2327013058

О компании:
МКУ «УКС МОБР» ИНН 2327013058, ОГРН 1132363000175 зарегистрировано 12.03.2013 в регионе Краснодарский Край по адресу: 352750, Краснодарский кр, станица Брюховецкая, район Брюховецкий, улица Красная, 211. Статус: Действующее. Размер Уставного Капитала — руб.

Руководителем организации является: Начальник — Бандуров Виталий Григорьевич, ИНН . У организации 1 Учредитель. Основным направлением деятельности является «деятельность в области архитектуры, инженерных изысканий и предоставление технических консультаций в этих областях».

Рейтинг организации:
Высокий
  подробнее

ВНИМАНИЕ: для оценки рисков работы с данной организацией рекомендуем отчет

Должная осмотрительность ?

Статус: ?
Действующее

Дата регистрации: По данным портала ЗАЧЕСТНЫЙБИЗНЕС

?
По данным портала ЗАЧЕСТНЫЙБИЗНЕС

12.03.2013
Размещенные вакансии

ОГРН  ?	1132363000175    присвоен: 12.03.2013
ИНН  ?	2327013058
КПП  ?	232701001
ОКПО  ?	10122371
ОКТМО  ?	03610407101

Реквизиты для договора 
?
 …Скачать

Проверить блокировку cчетов 
?

Контактная информация +7(8… Посмотреть
?

Отзывы об организации 
?: 0   Написать отзыв

Юридический адрес: ?
По данным портала ЗАЧЕСТНЫЙБИЗНЕС
352750, Краснодарский кр, станица Брюховецкая, район Брюховецкий, улица Красная, 211
получен 04.03.2016
зарегистрировано по данному адресу:
По данным портала ЗАЧЕСТНЫЙБИЗНЕС

По данным портала ЗАЧЕСТНЫЙБИЗНЕС
Руководитель Юридического Лица ?По данным портала ЗАЧЕСТНЫЙБИЗНЕС
НачальникПо данным портала ЗАЧЕСТНЫЙБИЗНЕС

Бандуров Виталий Григорьевич

ИНН ?	По данным портала ЗАЧЕСТНЫЙБИЗНЕС
действует с	По данным портала ЗАЧЕСТНЫЙБИЗНЕС 09.06.2018

Учредители ? ()

По данным портала ЗАЧЕСТНЫЙБИЗНЕС По данным портала ЗАЧЕСТНЫЙБИЗНЕС АДМИНИСТРАЦИЯ МУНИЦИПАЛЬНОГО ОБРАЗОВАНИЯ БРЮХОВЕЦКИЙ РАЙОН По данным портала ЗАЧЕСТНЫЙБИЗНЕС 12.03.2013 , ИНН

Основной вид деятельности: ?По данным портала ЗАЧЕСТНЫЙБИЗНЕС
71.1 деятельность в области архитектуры, инженерных изысканий и предоставление технических консультаций в этих областях

Дополнительные виды деятельности:

Единый Реестр Проверок (Ген. Прокуратуры РФ) ?

Реестр недобросовестных поставщиков: ?
По данным портала ЗАЧЕСТНЫЙБИЗНЕС

не числится.

Реестр операторов, осуществляющих обработку персональных данных (Данные РКН) ?

Регистрационный номер:	По данным портала ЗАЧЕСТНЫЙБИЗНЕС 23-16-006129 от По данным портала ЗАЧЕСТНЫЙБИЗНЕС 17.10.2016
Дата начала обработки:	По данным портала ЗАЧЕСТНЫЙБИЗНЕС 25.02.2013

Налоговый орган ?
По данным портала ЗАЧЕСТНЫЙБИЗНЕС
Межрайонная Инспекция Федеральной Налоговой Службы № 4 По Краснодарскому Краю
Дата постановки на учет: По данным портала ЗАЧЕСТНЫЙБИЗНЕС
12.03.2013

Регистрация во внебюджетных фондах

Фонд	Рег. номер	Дата регистрации
ПФР  ?	033029023103	По данным портала ЗАЧЕСТНЫЙБИЗНЕС 21.03.2013
ФСС  ?	231242287123121	По данным портала ЗАЧЕСТНЫЙБИЗНЕС 14.03.2013

Коды статистики

ОКАТО  ?	03210807001
ОКОГУ  ?	4210007
ОКОПФ  ?	75404
ОКФС  ?	14

Финансовая отчетность МКУ «УКС МОБР» ?

В качестве Поставщика: , на сумму

В качестве Заказчика: , на сумму

По данным портала ЗАЧЕСТНЫЙБИЗНЕС

Судебные дела МКУ «УКС МОБР» ?

найдено по ИНН: По данным портала ЗАЧЕСТНЫЙБИЗНЕС

найдено по наименованию (возможны совпадения): По данным портала ЗАЧЕСТНЫЙБИЗНЕС

По данным портала ЗАЧЕСТНЫЙБИЗНЕС

Исполнительные производства МКУ «УКС МОБР»
?

найдено по наименованию и адресу (возможны совпадения): По данным портала ЗАЧЕСТНЫЙБИЗНЕС

По данным портала ЗАЧЕСТНЫЙБИЗНЕС

Лента изменений МКУ «УКС МОБР»
?

Не является участником проекта ЗАЧЕСТНЫЙБИЗНЕС ?

Больше информации об организации — в Премиум доступе

Выполнение расчетов

Вычисление обратной матрицы в Excel возможно только в том случае, если первичная матрица является квадратной, то есть количество строк и столбцов в ней совпадает. Кроме того, её определитель не должен быть равен нулю. Для вычисления применяется функция массива МОБР. Давайте на простейшем примере рассмотрим подобное вычисление.

Расчет определителя

Прежде всего, вычислим определитель, чтобы понять, имеет первичный диапазон обратную матрицу или нет. Это значение рассчитывается при помощи функции МОПРЕД.

1. Выделяем любую пустую ячейку на листе, куда будут выводиться результаты вычислений. Жмем на кнопку «Вставить функцию», размещенную около строки формул.
2. Запускается Мастер функций. В перечне записей, который он представляет, ищем «МОПРЕД», выделяем этот элемент и жмем на кнопку «OK».
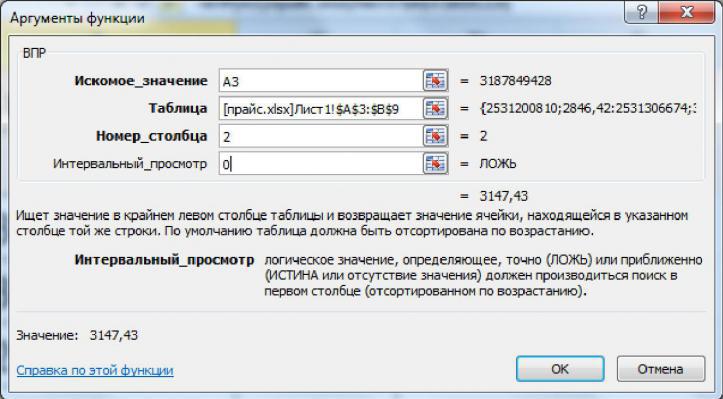
3. Открывается окно аргументов. Ставим курсор в поле «Массив». Выделяем весь диапазон ячеек, в котором расположена матрица. После того, как его адрес появился в поле, жмем на кнопку «OK».
4. Программа производит расчет определителя. Как видим, для нашего конкретного случая он равен – 59, то есть не тождественен нулю. Это позволяет сказать, что у данной матрицы существует обратная.

Расчет обратной матрицы

Теперь можно преступить к непосредственному расчету обратной матрицы.

1. Выделяем ячейку, которая должна стать верхней левой ячейкой обратной матрицы. Переходим в Мастер функций, кликнув по значку слева от строки формул.
2. В открывшемся списке выбираем функцию МОБР. Жмем на кнопку «OK».
3. В поле «Массив», открывшегося окна аргументов функции, устанавливаем курсор. Выделяем весь первичный диапазон. После появления его адреса в поле, жмем на кнопку «OK».
4. Как видим, появилось значение только в одной ячейке, в которой была формула. Но нам нужна полноценная обратная функция, поэтому следует скопировать формулу в другие ячейки. Выделяем диапазон, равнозначный по горизонтали и вертикали исходному массиву данных. Жмем на функциональную клавишу F2, а затем набираем комбинацию Ctrl+Shift+Enter. Именно последняя комбинация предназначена для обработки массивов.
5. Как видим, после этих действий обратная матрица вычислена в выделенных ячейках.

На этом расчет можно считать завершенным.

Если вы производите расчет определителя и обратной матрицы только при помощи ручки и бумаги, то над этим вычислением, в случае работы над сложным примером, можно ломать голову очень долго. Но, как видим, в программе Эксель данные вычисления производятся очень быстро, независимо от сложности поставленной задачи. Для человека, который знаком с алгоритмом подобных расчетов в этом приложении, все вычисление сводится к чисто механическим действиям.

Мы рады, что смогли помочь Вам в решении проблемы.

Помогла ли вам эта статья?

Нахождение обратной матрицы всегда вызывало большие затруднения у учащихся, так как это был очень трудоемкий процесс. И вот такое задание вполне по силам EXCEL.  

Прежде всего, уясним одно правило:  Матрица имеет обратную только тогда, когда ее определитель не равен нулю.  А вот и задание: найдите матрицу, обратную к матрице А, где

Вычислять определитель этой матрицы мы умеем. Я его уже вычислил.

Он оказался равен -4, а  это значит, что у нашей матрицы есть обратная (если бы определитель оказался равен нулю, то мы сказали бы что матрица не имеет обратную и немедленно прекратили все вычисления). Теперь отметим ячейку, с которой начнем записывать ответ. Я отметил ячейку E1.  Нажимаем Формулы, затем Математические и в появившемся окне находим  МОБР

После нажатия появляется вот такое окно, в котором надо вписать адреса ячеек, в которых находятся элементы матрицы  в Массив

У нас элементы записаны в ячейки начиная с А1 и заканчивая в С3 , поэтому так и записываем (смотрите картинку)

Если все сделали правильно, то автоматически заполнится место, обведенное красным и запишется ответ, который обведен черным. В таком виде ответ трудно переваривать и поэтому нажимаем ОК.  В ячейке, которую мы застолбили под ответ, появилось число 3,  Это только первый элемент полученной обратной матрицы.

Чтобы виден был весь ответ, выполняем следующие действия: Начиная с  ячейки Е1 выделяем три строчки и три столбца (именно столько было у исходной матрицы и столько же будет у обратной)

нажимаем клавишу F2,  а затем на одновременно на три клавиши  Ctrl+Shift+Enter.

В выделенном месте появляются, теперь уже все, элементы обратной матрицы. Если Вы сохраните этот документ, то в следующий раз можете воспользоваться плодами своего труда. Так, меняя элементы исходной матрицы, Вы автоматически получаете для нее же обратную матрицу.

На этом все. Крепких вам знаний.

Рубрика: EXCEL в помощь, Статьи. Метки: EXCEL, ИКТ, матрица, обратная матрица

Пример функции МОПРЕД для вычисления детерминанта матрицы в Excel

Примеры использования функции МОПРЕД в Excel.

Пример 1. Одним из свойств матриц является то, что определитель (детерминант) исходной матрицы соответствует определителю транспонированной матрицы. Доказать справедливость этого суждения с использованием средств Excel.

Вид таблицы с данными:

Для получения транспонированной матрицы выделим соответствующий по количеству строк и столбцов диапазон ячеек и используем следующую формулу (формула массива CTRL+SHIFT+Enter):

=ТРАНСП(A2:C4)

A2:A4 – диапазон ячеек со значениями исходной матрицы.

В результате получим:

Рассчитаем детерминант для каждой матрицы отдельно:

=МОПРЕД(A2:C4)

=МОПРЕД(E2:G4)

A2:C4 и E2:G4 – диапазоны ячеек со значениями исходной и транспонированной матриц соответственно.

Полученные результаты:

Во избежание промежуточных вычислений можно было использовать формулу массива CTRL+SHIFT+Enter:

=МОПРЕД(ТРАНСП(A2:C4))

Результат вычислений:

В результате вычислений формул Excel детерминант – доказан!

Пример: меняем местами строки и столбцы

Очень часто может появляться ситуация, когда нужно строки и колонки менять местами. Такая операция называется транспонированием. С помощью массивов функций это делать невероятно легко. Представим, у нас есть такой двумерный массив, расположенный по вертикали.

14

Нам нужно выделить диапазон данных, в котором будет размещаться готовая таблица. Поскольку в нашем примере 8 рядов и 2 колонки, то соответственно нужно выделять наоборот, 8 колонок и 2 ряда. 

После этого надо ввести формулу =ТРАНСП, введя в качестве аргумента функции A1:B8.

15

После этого нажимаем вышеуказанную комбинацию клавиш для создания формулы массива, после чего получаем транспонированную таблицу.

16

3 .3 . Пример макроса

Второй способ опирается на рекуррентное соотношение,
связывающее два соседних члена в ряду

Для того чтобы воспользоваться этим соотношением, надо
организовать на листе рекуррентную процедуру. Например, так, как
показано на Рис. 42

Рис.42
Вычисление функции E
1 (x
)
итерационным способом

Один шаг итерации – это переход от значений в области
J2:J4
к значениям в области
L2:L4
. Для того, чтобы сделать следующую
итерацию, нужно скопировать значения, получившиеся в области
L2:L4
и вставить их в область
J2:J4
. При этом вставлять нужно только
величины, без формул. Величины в области H2:H4

дают исходные значения для начала итерации.Повторяя многократно
операцию Copy-Paste Special
, можно получить в
ячейке L4
искомое значение. Однако
копирование – это скучное занятие и его было бы неплохо
автоматизировать. Для этого можно написать макрос.

Проще всего начать создание макроса через запись команд,
выполняемых на листе. Для этого идем в раздел меню Tools–Macro–Record
New Macro
. Появляется окно (Рис. 43
), в котором можно указать имя
макроса и где он будет расположен.

Рис.43
Запись макро

После нажатия OK
начинается
запись всех действий, выполняемых на листе. Когда все, что нужно
сохранено в макросе, запись надо остановить командой
Tools–Macro–Stop Recording
. Результат можно увидеть, зайдя в
редактор Visual Basic

.

Рис.44
Редактор Visual Basic

На Рис.

Рис.45
Функция IntExp

На Рис. 45
приведен
код этой функции и пример обращения к
ней.

Мы не будем рассказывать о программировании на VBA, т.к.
это очень большой и сложный вопрос. Самостоятельно его можно изучить по
имеющимся в сети многочисленным пособиям, например,
.

VBA – это довольно медленный язык и он плохо подходит
для больших вычислений. Например, не стоит писать на этом языке
процедуру для PCA декомпозиции – на больших массивах она будет считать
очень долго. Правильнее рассматривать Excel и VBA как интерфейс (front
end) для ввода и вывода данных, которые затем передаются в динамическую
библиотеку (DLL), написанную на быстром языке, таком как C++ (back end).
Именно эта концепция и была реализована в надстройках
Fitter
и
Chemometrics
.

Подробнее об использовании пользовательских функций для
расширения возможностей надстройки Chemometrics

можно прочитать
.