Пример выполнения корреляционного анализа в excel

9.1.6. Корреляция, регрессия и причинность

Корреляция и регрессия — инструменты исследования связи, или согласованности двух переменных. Их возможности ограниченны. Сами по себе они никогда не смогут ничего сказать о направлении связи между переменными. Влияет ли уровень оптимизма на продолжительность жизни или, напротив, прогноз состояния организма, каким-то образом воспринимаемый его владельцем, влияет на уровень оптимизма — вопрос, на который нельзя ответить исходя только из корреляционных и регрессионных коэффициентов. Если ответ и возможен, то только с опорой на тонкие аспекты экспериментального дизайна.

>> следующий параграф>>

Здесь также можно различать двухсторонние и односторонние гипотезы, как в случае Т-критерия (см. подпараграф 7.1.5).

Для коэффициента корреляции так же, как и для других статистик, возможен расчет доверительных интервалов, показывающих, какие возможные значения истинной корреляции согласуются с выборочным. Смысл доверительного интервала тот же, что и в разобранных выше случаях, но техника расчета сложнее, поэтому мы не будем ее здесь давать.

В подпараграфе 9.3.1 практикума мы разберем эти операции на конкретном примере. Мы рекомендуем читателю сначала выполнить практическое задание, а затем вернуться к данному пункту.

В главе 7 ​\( S_{total} \)​ обозначала у нас сумму квадратов, включая сумму константы, здесь же \( S_{total} \) ее не включает. Это не наш недосмотр, так обозначаются суммы в соответствующих таблицах SPSS, на которые мы здесь ориентируемся. Чтобы уменьшить риск путаницы, мы в первом случае используем заглавную букву ’T’.

Не будем забывать, что наши данные содержат вклад случайных обстоятельств, поэтому при повторении исследования мы можем получить иные коэффициенты.

Как восстановить доступ к аккаунту

Если пароль к учетной записи Гугл потерян, то рекомендуем воспользоваться сервисом Google Account Recovery. Алгоритм действий следующий:

1. Переходят на страницу услуги. Процедуру удобнее проводить на ПК.
2. В открывшемся окне выбирают диалог «Не помню пароль». Жмут кнопку «Затрудняюсь ответить».
3. Отмечают режим восстановления при помощи сообщения на привязанный телефон. Приходит СМС с цифровым кодом подтверждения.
4. В открывшемся окне вводят комбинацию, жмут ОК.
5. Сервис советует придумать и ввести новый пароль к учетной записи. Изменения сохраняют.

Как вы можете рассчитать корреляцию с помощью Excel? — 2019

a:

Корреляция измеряет линейную зависимость двух переменных. Измеряя и связывая дисперсию каждой переменной, корреляция дает представление о силе взаимосвязи. Или, говоря иначе, корреляция отвечает на вопрос: сколько переменная A (независимая переменная) объясняет переменную B (зависимую переменную)?

Формула корреляции

Корреляция объединяет несколько важных и связанных статистических понятий, а именно дисперсию и стандартное отклонение. Разница — дисперсия переменной вокруг среднего, а стандартное отклонение — квадратный корень дисперсии.

Формула:

Поскольку корреляция требует оценки линейной зависимости двух переменных, то, что действительно необходимо, — это выяснить, какая сумма ковариации этих двух переменных и в какой степени такая ковариация отраженные стандартными отклонениями каждой переменной в отдельности.

Общие ошибки с корреляцией

Самая распространенная ошибка — предполагать, что корреляция, приближающаяся +/- 1, статистически значима. Считывание, приближающееся +/- 1, безусловно увеличивает шансы на фактическую статистическую значимость, но без дальнейшего тестирования это невозможно узнать.

Статистическое тестирование корреляции может усложняться по ряду причин; это совсем не так просто. Критическое предположение о корреляции состоит в том, что переменные независимы и связь между ними является линейной.

Вторая наиболее распространенная ошибка — забыть нормализовать данные в единую единицу. Если вычислять корреляцию по двум бетам, то единицы уже нормализованы: сама бета является единицей

Однако, если вы хотите скорректировать акции, важно, чтобы вы нормализовали их в процентном отношении, а не изменяли цены. Это происходит слишком часто, даже среди профессионалов в области инвестиций

Для корреляции цен на акции вы, по сути, задаете два вопроса: каково возвращение за определенное количество периодов и как этот доход коррелирует с возвратом другой безопасности за тот же период? Это также связано с тем, что корреляция цен на акции затруднена: две ценные бумаги могут иметь высокую корреляцию, если доход составляет ежедневно процентов за последние 52 недели, но низкая корреляция, если доход ежемесячно > изменения за последние 52 недели. Какая из них лучше»? На самом деле нет идеального ответа, и это зависит от цели теста. ( Улучшите свои навыки excel, пройдя курс обучения Excel в Академии Excel. ) Поиск корреляции в Excel

Существует несколько методов расчета корреляции в Excel

Самый простой способ — получить два набора данных и использовать встроенную формулу корреляции:

Это удобный способ расчета корреляции между двумя наборами данных. Но что, если вы хотите создать корреляционную матрицу во множестве наборов данных? Для этого вам нужно использовать плагин анализа данных Excel. Плагин можно найти на вкладке «Данные» в разделе «Анализ».

Выберите таблицу возвратов. В этом случае наши столбцы имеют названия, поэтому мы хотим установить флажок «Ярлыки в первой строке», поэтому Excel знает, как обрабатывать их как заголовки. Затем вы можете выбрать вывод на том же листе или на новом листе.

Как только вы нажмете enter, данные будут автоматически сделаны. Вы можете добавить текст и условное форматирование, чтобы очистить результат.

Распространенные заблуждения

Корреляция и причинность

Традиционное изречение, что « корреляция не подразумевает причинно-следственную связь », означает, что корреляция не может использоваться сама по себе для вывода причинной связи между переменными. Это изречение не следует понимать как то, что корреляции не могут указывать на возможное существование причинно-следственных связей. Однако причины, лежащие в основе корреляции, если таковые имеются, могут быть косвенными и неизвестными, а высокие корреляции также пересекаются с отношениями идентичности ( тавтологиями ), где не существует причинного процесса. Следовательно, корреляция между двумя переменными не является достаточным условием для установления причинной связи (в любом направлении).

Корреляция между возрастом и ростом у детей довольно прозрачна с точки зрения причинно-следственной связи, но корреляция между настроением и здоровьем людей менее очевидна. Приводит ли улучшение настроения к улучшению здоровья, или хорошее здоровье приводит к хорошему настроению, или и то, и другое? Или в основе обоих лежит какой-то другой фактор? Другими словами, корреляция может рассматриваться как свидетельство возможной причинной связи, но не может указывать на то, какой может быть причинная связь, если таковая имеется.

Простые линейные корреляции

Четыре набора данных с одинаковой корреляцией 0,816

Коэффициент корреляции Пирсона указывает на силу линейной связи между двумя переменными, но его значение, как правило, не полностью характеризует их взаимосвязь. В частности, если условное среднее из дано , обозначается , не является линейным в , коэффициент корреляции будет не в полной мере определить форму .
Y{\ displaystyle Y}Икс{\ displaystyle X}E⁡(Y∣Икс){\ displaystyle \ operatorname {E} (Y \ mid X)}Икс{\ displaystyle X}E⁡(Y∣Икс){\ displaystyle \ operatorname {E} (Y \ mid X)}

Прилегающие изображение показывает разброс участков из квартет энскомбы , набор из четырех различных пар переменных , созданный Фрэнсис Анскомбами . Четыре переменные имеют одинаковое среднее значение (7,5), дисперсию (4,12), корреляцию (0,816) и линию регрессии ( y  = 3 + 0,5 x ). Однако, как видно на графиках, распределение переменных сильно отличается. Первый (вверху слева), кажется, распределен нормально и соответствует тому, что можно было бы ожидать, рассматривая две коррелированные переменные и следуя предположению о нормальности. Второй (вверху справа) не распространяется нормально; Хотя можно наблюдать очевидную связь между двумя переменными, она не является линейной. В этом случае коэффициент корреляции Пирсона не указывает на то, что существует точная функциональная связь: только степень, в которой эта связь может быть аппроксимирована линейной зависимостью. В третьем случае (внизу слева) линейная зависимость идеальна, за исключением одного выброса, который оказывает достаточное влияние, чтобы снизить коэффициент корреляции с 1 до 0,816. Наконец, четвертый пример (внизу справа) показывает другой пример, когда одного выброса достаточно для получения высокого коэффициента корреляции, даже если связь между двумя переменными не является линейной.
у{\ displaystyle y}

Эти примеры показывают, что коэффициент корреляции, как сводная статистика, не может заменить визуальный анализ данных. Иногда говорят, что примеры демонстрируют, что корреляция Пирсона предполагает, что данные следуют нормальному распределению , но это неверно.

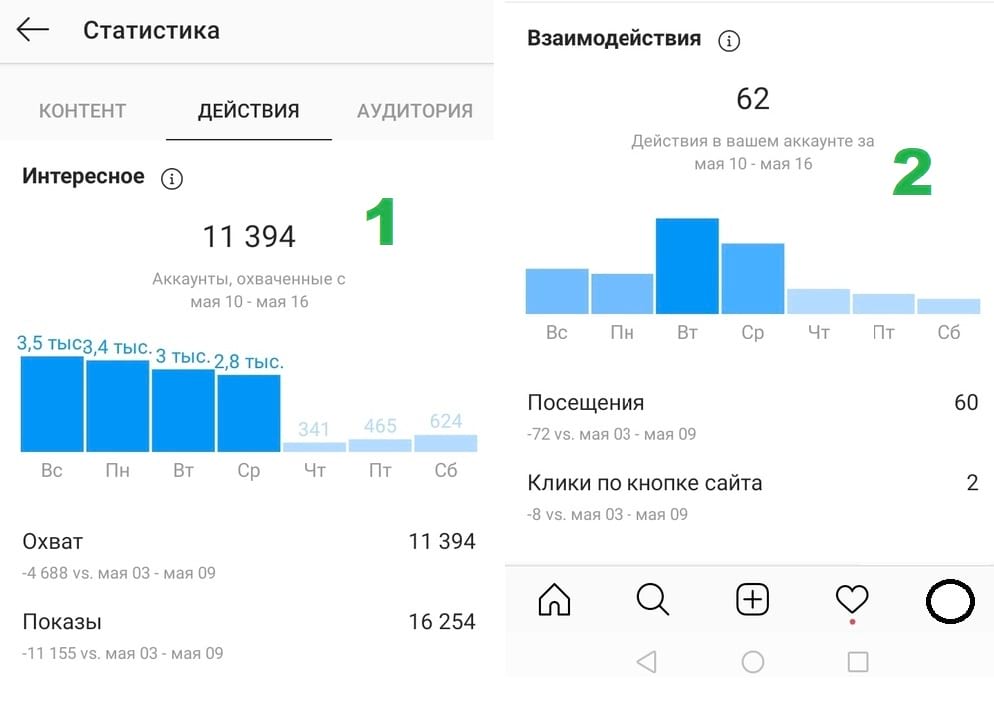
Отображение результатов

Результаты корреляционного анализа могут быть представлены в текстовом и графическом видах. В первом случае они представляются как коэффициент корреляции, во втором — в виде диаграммы разброса.

При отсутствии корреляции между параметрами точки на диаграмме расположены хаотично, средняя степень связи характеризуется большей степенью упорядоченности и характеризуется более-менее равномерной удаленностью нанесенных отметок от медианы. Сильная связь стремится к прямой и при r=1 точечный график представляет собой ровную линию. Обратная корреляция отличается направленностью графика из левого верхнего в нижний правый, прямая — из нижнего левого в верхний правый угол.

Hard Reset средствами самой системы Android

§ 8. Методика вычисления выборочного коэффициента корреляции

Пусть требуется
по данным корреляционной таблицы
вычислить выборочный коэффициент
корреляции. Можно значительно упростить
расчет, если перейти к условным вариантам
(при этом величина r_в
не изменится)

u_i=(x_i—С₁)/h₁
и υ_j=(y_j—С₂)/h₂.

В этом случае
выборочный коэффициент корреляции
вычисляют по формуле

.

Величины u,
υ

и
можно найти методом произведений (см.
гл. XVII, § 4), а при малом числе данных—
непосредственно исходя из определений
этих величин. Остается указать способ
вычисления ,
где —
частота пары
условных вариант (u,
υ).

Можно доказать,
что справедливы формулы (см. пояснение
в конце параграфа):

,
где
,

,
где
.

Для контроля
целесообразно выполнить расчеты по
обеим формулам и сравнить результаты;
их совпадение свидетельствует о
правильности вычислений.

Покажем на примере,
как пользоваться приведенными формулами.

Пример 1.
Вычислить ^ «по»» П0
данным корреляционной табл. 14.

Таблица 14

Y	X	ny
10	20	30	40	50	60
15	5	7	—	—	—	—	12
25	—	20	23	—	—	—	43
35	—	—	30	47	2	—	79
45	—	—	10	11	20	6	47
55	—	—	—	9	7	3	19
nx	5	27	63	67	29	9	n=200

Решение. Перейдем
к условным вариантам: u_i=(x_i—С₁)/h₁
= = (x_i
—40)/10 (в качестве
ложного нуля С₁
взята варианта х=40.
расположенная
примерно в середине вариационного ряда;
шаг h₁
равен разности
между двумя соседними вариантами: 20—10
= 10) и υ_j=(y_j—С₂)/h₂
= (y_j
—35)/10 (в качестве
ложного нуля С₂
взята варианта у =35, расположенная в
середине вариационного ряда; шаг h₂
равен разности между двумя соседними
вариантами: 25—15=10).

Составим
корреляционную таблицу в условных
вариантах. Практически это делают так:
в первом столбце вместо ложного нуля
С₂
(варианты 35) пишут 0; над нулем последовательно
записывают —1,
—2; под нулем пишут 1, 2. В первой строке
вместо ложного нуля С₁
(варианты 40) пишут 0; слева от нуля
последовательно записывают —1, —2, —3;
справа от нуля пишут 1, 2. Все остальные
данные переписывают из первоначальной
корреляционной таблицы. В итоге получим
корреляционную табл. 15 в условных
вариантах.

Таблица
15

υ			u	nυ
-3	-2	— 1	1	2
—2	5	7	—	—	—	—	12
—1	—	20	23	—	—	—	43
—	—	30	47	2	—	79
1	—	—	10	11	20	6	47
2	—	—	—	9	7	3	19
nu	5	27	63	67	29	9	n = 200

Теперь для вычисления
искомой суммы составим
расчетную табл. 16. Пояснения к составлению
табл. 16:

1. В каждой клетке,
в которой частота n_uυ
≠ 0, записывают
в правом верхнем углу произведение
частоты n_uυ
на варианту u.
Например, в
правых верхних углах клеток первой
строки записаны произведения: 5·(—3) =
—15; 7·(—2) = —14.

2. Складывают все
числа, помещенные в правых верхних углах
клеток одной строки и их сумму записывают
в клетку этой же строки столбца u.
Например, для первой строки
U
== —15+(—14)= —29.

3. Умножают варианту
υ
на U
и полученное произведение заци-сывают
в последнюю клетку той же строки, т. е.
в клетку столбца υU.
Например,
в первой строке таблицы υ
= —2,
U
= —29; следовательно, υU
= (—2)·(—29) = 58.

4. Наконец, сложив
все числа столбца υU,
получают сумму
,
которая равна искомой сумме .
Например, для табл.
16 имеем
=
169; следовательно, искомая сумма =
169.

Таблица 16

υ	u ч 1	U= =	υU
-3	-2	—1	1	2
-2	—15 5 -10	-14 7 -14	—	—	—	—	—29	58
-1	—	—40 20 -20	—23 23 —23	—	—	—	-63	63
—	—	-30 30	47	2 2	—	—28
1	—	—	—10 10 10	11 11	20 20 20	12 6 6	22	22
2	—	—	—	9 18	7 7 14	6 3 6	13	26
V= =	—10	-34	—13	29	34	12		= =169
uV	30	68	13	34	«	==169	Контроль

Для контроля
аналогичные вычисления производят по
столбцам:

произведения n_uυυ
записывают в левый нижний угол клетки,
содержащей частоту n_uυυ
≠ 0; все числа,
помещенные в левых нижних углах клеток
одного столбца, складывают и их сумму
записывают в строку V;
далее умножают каждую варианту u
на V
и результат записывают в клетках
последней строки.

Наконец, сложив
все числа последней строки, получают
сумму
,
которая также равна искомой сумме .
Например, для табл.
16 имеем
=
169; следовательно,= 169.

Теперь, когда мы
научились вычислять ,
приведем пример на отыскание выборочного
коэффициента корреляции.

Шесть тысяч четыреста пятьдесят три рубля шестьдесят три копейки

Критерии и методы

КРИТЕРИЙ СПИРМЕНА

Коэффициент ранговой корреляции Спирмена – это непараметрический метод, который используется с целью статистического изучения связи между явлениями. В этом случае определяется фактическая степень параллелизма между двумя количественными рядами изучаемых признаков и дается оценка тесноты установленной связи с помощью количественно выраженного коэффициента.

Чарльз Эдвард Спирмен

1. История разработки коэффициента ранговой корреляции

Данный критерий был разработан и предложен для проведения корреляционного анализа в 1904 году Чарльзом Эдвардом Спирменом, английским психологом, профессором Лондонского и Честерфилдского университетов.

2. Для чего используется коэффициент Спирмена?

Коэффициент ранговой корреляции Спирмена используется для выявления и оценки тесноты связи между двумя рядами сопоставляемых количественных показателей. В том случае, если ранги показателей, упорядоченных по степени возрастания или убывания, в большинстве случаев совпадают (большему значению одного показателя соответствует большее значение другого показателя — например, при сопоставлении роста пациента и его массы тела), делается вывод о наличии прямой корреляционной связи. Если ранги показателей имеют противоположную направленность (большему значению одного показателя соответствует меньшее значение другого — например, при сопоставлении возраста и частоты сердечных сокращений), то говорят об обратной связи между показателями.

1. Коэффициент корреляции Спирмена обладает следующими свойствами:
2. Коэффициент корреляции может принимать значения от минус единицы до единицы, причем при rs=1 имеет место строго прямая связь, а при rs= -1 – строго обратная связь.
3. Если коэффициент корреляции отрицательный, то имеет место обратная связь, если положительный, то – прямая связь.
4. Если коэффициент корреляции равен нулю, то связь между величинами практически отсутствует.
5. Чем ближе модуль коэффициента корреляции к единице, тем более сильной является связь между измеряемыми величинами.

3. В каких случаях можно использовать коэффициент Спирмена?

В связи с тем, что коэффициент является методом непараметрического анализа, проверка на нормальность распределения не требуется.

Сопоставляемые показатели могут быть измерены как в непрерывной шкале (например, число эритроцитов в 1 мкл крови), так и в порядковой (например, баллы экспертной оценки от 1 до 5).

Эффективность и качество оценки методом Спирмена снижается, если разница между различными значениями какой-либо из измеряемых величин достаточно велика. Не рекомендуется использовать коэффициент Спирмена, если имеет место неравномерное распределение значений измеряемой величины.

4. Как рассчитать коэффициент Спирмена?

Расчет коэффициента ранговой корреляции Спирмена включает следующие этапы:

1. Сопоставить каждому из признаков их порядковый номер (ранг) по возрастанию или убыванию.
2. Определить разности рангов каждой пары сопоставляемых значений (d).
3. Возвести в квадрат каждую разность и суммировать полученные результаты.
4. Вычислить коэффициент корреляции рангов по формуле:

Определить статистическую значимость коэффициента при помощи t-критерия, рассчитанного по следующей формуле:

5. Как интерпретировать значение коэффициента Спирмена?

При использовании коэффициента ранговой корреляции условно оценивают тесноту связи между признаками, считая значения коэффициента меньше 0,3 — признаком слабой тесноты связи; значения более 0,3, но менее 0,7 — признаком умеренной тесноты связи, а значения 0,7 и более — признаком высокой тесноты связи.

Также для оценки тесноты связи может использоваться шкала Чеддока:

_xy
Теснота (сила) корреляционной связи
менее 0.3
слабая
от 0.3 до 0.5
умеренная
от 0.5 до 0.7
заметная
от 0.7 до 0.9
высокая
более 0.9
весьма высокая

Статистическая значимость полученного коэффициента оценивается при помощи t-критерия Стьюдента. Если расчитанное значение t-критерия меньше табличного при заданном числе степеней свободы, статистическая значимость наблюдаемой взаимосвязи — отсутствует. Если больше, то корреляционная связь считается статистически значимой.

Пошаговая регрессия

_12mijxjxiy

На втором шаге строится уравнение регрессии с одной переменной, имеющей максимальный по абсолютной величине парный коэффициент корреляции с результативным признаком.

На третьем шаге в модель вводится новая переменная, имеющая наибольшее по абсолютной величине значение частного коэффициента корреляции с зависимой переменной при фиксированном влиянии ранее введенной переменной.
При введении в модель дополнительного фактора коэффициент детерминации должен возрастать, а остаточная дисперсия уменьшаться. Если этого не происходит, т. е. коэффициент множественной детерминации увеличивается незначительно, то ввод нового фактора признается нецелесообразным.

Пример №1. По 20 предприятиям региона изучается зависимость выработки продукции на одного работника y (тыс. руб.) от удельного веса рабочих высокой квалификации в общей численности рабочих x1 (% от стоимости фондов на конец года) и от ввода в действие новых основных фондов x2 (%).

Y	X1	X2
6	10	3,5
6	12	3,6
7	15	3,9
7	17	4,1
7	18	4,2
8	19	4,5
8	19	5,3
9	20	5,3
9	20	5,6
10	21	6
10	21	6,3
11	22	6,4
11	23	7
12	25	7,5
12	28	7,9
13	30	8,2
13	31	8,4
14	31	8,6
14	35	9,5
15	36	10

Требуется:

1. Построить корреляционное поле между выработкой продукции на одного работника и удельным весом рабочих высокой квалификации. Выдвинуть гипотезу о тесноте и виде зависимости между показателями X1 и Y .
2. Оценить тесноту линейной связи между выработкой продукции на одного работника и удельным весом рабочих высокой квалификации с надежностью 0,9.
3. Рассчитать коэффициенты линейного уравнения регрессии для зависимости выработки продукции на одного работника от удельного веса рабочих высокой квалификации.
4. Проверить статистическую значимость параметров уравнения регрессии с надежностью 0,9 и построить для них доверительные интервалы.
5. Рассчитать коэффициент детерминации. С помощью F -критерия Фишера оценить статистическую значимость уравнения регрессии с надежностью 0,9.
6. Дать точечный и интервальный прогноз с надежностью 0,9 выработки продукции на одного работника для предприятия, на котором высокую квалификацию имеют 24% рабочих.
7. Рассчитать коэффициенты линейного уравнения множественной регрессии и пояснить экономический смысл его параметров.
8. Проанализировать статистическую значимость коэффициентов множественного уравнения с надежностью 0,9 и построить для них доверительные интервалы.
9. Найти коэффициенты парной и частной корреляции. Проанализировать их.
10. Найти скорректированный коэффициент множественной детерминации. Сравнить его с нескорректированным (общим) коэффициентом детерминации.
11. С помощью F -критерия Фишера оценить адекватность уравнения регрессии с надежностью 0,9.
12. Дать точечный и интервальный прогноз с надежностью 0,9 выработки продукции на одного работника для предприятия, на котором высокую квалификацию имеют 24% рабочих, а ввод в действие новых основных фондов составляет 5%.
13. Проверить построенное уравнение на наличие мультиколлинеарности по: критерию Стьюдента; критерию χ2. Сравнить полученные результаты.

Решение проводим с помощью калькулятора. Далее приводится ход решения п.13.

Матрица парных коэффициентов корреляции R:

—	y	x1	x2
y	1	0.97	0.991
x1	0.97	1	0.977
x2	0.991	0.977	1

_{ixjxix1 x2yxiyx1критнаблкритyx2наблкритx1x22}Тестирование и устранение мультиколлинеарности222_табл2_табл2Определяем обратную матрицу-1

D =	55,365 -2,256 -52,656 -2,256 22,386 -19,642 -52,656 -19,642 72,373

_{kk12kТабл12Табл1табл2табл13табл2}Частные коэффициенты корреляции_{ijyx1 /x2критнабл121yx2 /x1наблкрит21212}

Пример №2. По 30 наблюдениям матрица парных коэффициентов корреляции оказалась следующей:

	y	x1	x2	x3
y	1,0
x1	0,30	1,0
x2	0,60	0,10	1,0
x3	0,40	0,15	0,80	1,0

уравнение регрессии в стандартном масштабе

Задачи, виды и показатели корреляционно-регрессионного анализа

Задачи КРА заключаются в:

• идентификации наиболее значимых факторов влияния на конкретный показатель деятельности предприятия;
• количественном измерении тесноты выявленных связей между показателями;
• определении неизвестных причин возникновения связей;
• всесторонней оценке факторов, которые признаны наиболее важными для рассматриваемого показателя;
• выведении формулы уравнения регрессии;
• составлении прогноза возможного результата деятельности при изменении ключевых связанных факторов с учетом возможного влияния других факторных признаков.

КРА подразумевает использование нескольких видов корреляционных и регрессионных методов. Зависимости выявляются при помощи корреляций таких типов:

• парная, если связь устанавливается с участием двух признаков;
• частная – взаимосвязь оценивается между искомым показателем и одним из ключевых факторов, при этом условием задается постоянное значение комплекса других факторов (то есть числовое выражение всех остальных факторов в любых ситуациях будет приниматься за определенную неизменную величину);
• множественная – основу исследования составляет влияние на показатель деятельности не одного фактора, а сразу нескольких критериев (двух и более).

СПРАВОЧНО! Выявленные показатели степени тесноты связей отражаются коэффициентом корреляции.

На выбор коэффициента влияет шкала измерения признаков:

1. Шкала номинальная, которая предназначена для приведения описательных характеристик объектов.
2. Шкала ординальная нужна для вычисления степени упорядоченности объектов в привязке к одному и более признакам.
3. Шкала количественная используется для отражения количественных значений показателей.

Регрессионный анализ пользуется методом наименьших квадратов. Регрессия может быть линейной и множественной. Линейный тип предполагает модель из связей между двумя параметрами. Например, при наличии таких двух критериев, как урожайность клубники и полив, понятно, что именно объем поступающей влаги будет влиять на объем выращенной и собранной клубники. Если полив будет чрезмерным, то урожай пропадет. Урожайность же клубники никак не может воздействовать на систему полива.

Множественная регрессия учитывает более двух факторов одновременно. В случае с клубникой при оценке ее урожайности могут использоваться факторы полива, плодородности почвы, температурного режима, отсутствия слизняков, сортовые особенности, своевременность внесения удобрений. Все перечисленные показатели в совокупности оказывают комплексное воздействие на искомое значение – урожайность ягод.

Система показателей анализа формируется критериями классификации. Например, при экстенсивном типе развития бизнеса в качестве показателей могут выступать такие факторы:

• количество сотрудников;
• число заключенных договоров за отчетный период;
• посевные площади;
• прирост поголовья скота;
• расширение дилерской сети;
• объем основных фондов.

При интенсивном типе развития могут применяться следующие показатели:

• производительность труда;
• рентабельность;
• урожайность;
• фондоотдача;
• ликвидность;
• средний объем поставок в отчетном периоде по одному договору.

Выборочный коэффициент корреляции

Коэффициент корреляции обычно рассчитывают по выборке. Значит, у аналитика в распоряжении не истинное значение, а оценка, которая всегда ошибочна. Если выборка была репрезентативной, то истинное значение коэффициента корреляции находится где-то относительно недалеко от оценки. Насколько далеко, можно определить через доверительные интервалы.

Согласно Центральное Предельной Теореме распределение оценки любого показателя стремится к нормальному с ростом выборки. Но есть проблемка. Распределение коэффициента корреляции вблизи придельных значений не является симметричным. Ниже пример распределения при истинном коэффициенте корреляции ρ = 0,86.

Предельное значение не дает выйти за 1 и, как бы «поджимает» распределение справа. Симметричная ситуация наблюдается, если коэффициент корреляции близок к -1.

В общем рассчитывать на свойства нормального распределения нельзя. Поэтому Фишер предложил провести преобразование выборочного коэффициента корреляции по формуле:

Распределение z для тех же r имеет следующий вид.

Намного ближе к нормальному. Стандартная ошибка z равна:

Далее исходя из свойств нормального распределения несложно найти верхнюю и нижнюю границы доверительного интервала для z. Определим квантиль стандартного нормального распределения для заданной доверительной вероятности, т.е. количество стандартных отклонений от центра распределения.

c_γ – квантиль стандартного нормального распределения;N-1 – функция обратного стандартного распределения;γ – доверительная вероятность (часто 95%).Затем рассчитаем границы доверительного интервала.

Нижняя граница z:

Верхняя граница z:

Теперь обратным преобразованием Фишера из z вернемся к r.Нижняя граница r:

Верхняя граница r:

Это была теоретическая часть. Переходим к практике расчетов.

Проблемы применения

В основе корреляционно-регрессионного анализа лежат следующие предположения:

• Наблюдения считаются независимыми (пятикратное выпадение «орла» никак не влияет на результат следующего подбрасывания монетки).
• В корреляционном анализе обе переменные рассматриваются как случайные. В регрессионном – только одна (зависимая).
• При проверке гипотезы должно соблюдаться нормальное распределение. Изменение зависимой переменной должно быть одинаковым для каждой величины на оси абсцисс.
• Корреляционная диаграмма – это только первая проверка гипотезы о взаимоотношениях между двумя рядами параметров, а не конечный результат анализа.

Оставить комментарий