Коэффициент корреляции: что нужно знать, формула, пример расчёта в excel
Содержание:
- Hard Reset средствами самой системы Android
- Памятка
- Список литературы
- Самые интересные профессии для женщин
- пример
- Расчет коэффициента корреляции
- Имитация кирпича для внутренней отделки своими руками
- Несколько важных замечаний
- 9.1.2. Проверка статистических гипотез о связи переменных
- Корреляционные матрицы
- Литература
- Открытие загрузочной флешки через BIOS
- Вычисление коэффициента посредством мастера функций
Hard Reset средствами самой системы Android
Памятка
- Корреляция – это соотношение, взаимозависимость нескольких переменных.
- Связь бывает положительной и отрицательной.
- Коэффициент корреляции определяет степень взаимозависимости одной переменной от другой.
- На основании корреляции люди выдвигают гипотезы (часто ошибочные).
- Истинная причина корреляции порою скрыта под множеством факторов и внешних сил.
- Бывает ложная корреляционная зависимость.
- Раскладывая яйца по корзинам, помните о том, что они не должны коррелироваться друг с другом.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Использую для заработка
Список литературы
- Аблеева, А. М. Формирование фонда оценочных средств в условиях ФГОС / А. М. Аблеева, Г. А. Салимова // Актуальные проблемы преподавания социально-гуманитарных, естественно — научных и технических дисциплин в условиях модернизации высшей школы : материалы международной научно-методической конференции, 4-5 апреля 2014 г. / Башкирский ГАУ, Факультет информационных технологий и управления. — Уфа, 2014. — С. 11-14.
- Ганиева, А.М. Статистический анализ занятости и безработицы / А.М. Ганиева, Т.Н. Лубова // Актуальные вопросы экономико-статистического исследования и информационных технологий: сб. науч. ст.: посвящается к 40-летию создания кафедры «Статистики и информационных систем в экономике» / Башкирский ГАУ. — Уфа, 2011. — С. 315-316.
- Исмагилов, Р. Р. Творческая группа — эффективная форма организации научных исследований в высшей школе / Р. Р. Исмагилов, М. Х. Уразлин, Д. Р. Исламгулов // Научно-технический и научно-образовательный комплексы региона : проблемы и перспективы развития : материалы научно-практической конференции / Академия наук РБ, УГАТУ. — Уфа, 1999. — С. 105-106.
- Исламгулов, Д.Р. Компетентностный подход в обучении: оценка качества образования / Д.Р. Исламгулов, Т.Н. Лубова, И.Р. Исламгулова // Современный научный вестник. – 2015. – Т. 7. — № 1. – С. 62-69.
- Исламгулов, Д. Р. Научно-исследовательская работа студентов — важнейший элемент подготовки специалистов в аграрном вузе / Д. Р. Исламгулов // Проблемы практической подготовки студентов в вузе на современном этапе и пути их решения : сб. материалов науч.-метод. конф., 24 апреля 2007 года / Башкирский ГАУ. — Уфа, 2007. — С. 20-22.
- Лубова, Т.Н. Основа реализации федерального государственного образовательного стандарта – компетентностный подход / Т.Н. Лубова, Д.Р. Исламгулов, И.Р. Исламгулова// БЪДЕЩИТЕ ИЗСЛЕДОВАНИЯ – 2016: Материали за XII Международна научна практична конференция, 15-22 февруари 2016. – София: Бял ГРАД-БГ ООД, 2016. – Том 4 Педагогически науки. – C. 80-85.
- Лубова, Т.Н. Новые образовательные стандарты: особенности реализации / Т.Н. Лубова, Д.Р. Исламгулов // Современный научный вестник. – 2015. – Т. 7. — № 1. – С. 79-84.
- Лубова, Т.Н. Организация самостоятельной работы обучающихся / Т.Н. Лубова, Д.Р. Исламгулов // Реализация образовательных программ высшего образования в рамках ФГОС ВО: материалы Всероссийской научно-методической конференции в рамках выездного совещания НМС по природообустройству и водопользованию Федерального УМО в системе ВО. / Башкирский ГАУ. — Уфа, 2016. — С. 214-219.
- Лубова, Т.Н. Основа реализации федерального государственного образовательного стандарта – компетентностный подход / Т.Н. Лубова, Д.Р. Исламгулов, И.Р. Исламгулова // Современный научный вестник. – 2015. – Т. 7. — № 1. – С. 85-93.
- Саубанова, Л.М. Уровень демографической нагрузки / Л.М. Саубанова, Т.Н. Лубова // Актуальные вопросы экономико-статистического исследования и информационных технологий: сб. науч. ст.: посвящается к 40-летию создания кафедры «Статистики и информационных систем в экономике» / Башкирский ГАУ. — Уфа, 2011. — С. 321-322.
- Фахруллина, А.Р. Статистический анализ инфляции в России / А.Р. Фахруллина, Т.Н. Лубова // Актуальные вопросы экономико-статистического исследования и информационных технологий: сб. науч. ст.: посвящается к 40-летию создания кафедры «Статистики и информационных систем в экономике» / Башкирский ГАУ. — Уфа, 2011. — С. 323-324.
- Фархутдинова, А.Т. Рынок труда в Республике Башкортостан в 2012 году / А.Т. Фархутдинова, Т.Н. Лубова // Студенческий научный форум. Материалы V Международной студенческой электронной научной конференции: электронная научная конференция (электронный сборник). Российская академия естествознания. 2013.
Самые интересные профессии для женщин
Предрасположенность представительниц прекрасного пола к общению при работе с людьми и тяга к самовыражению делают их прекрасными работниками в сфере маркетинга, искусства, консультрирования, синхронного перевода, журналистики. Самыми интересными считаются следующие сферы занятости:
- Журналистика. Обработка и сбор информации, предоставление ее широкой аудитории, общение с интересными людьми — все это делает данную специализацию идеально подходящей для девушек, жаждущих общения, стремящихся к саморазвитию.
- Психология. Подавляющему большинству женщин свойственная явная эмпатия, сопереживание, сочувствие. Такие качества присущи хорошему психологу, способному поставить себя на место другого человека, чтобы разобраться в его эмоциях, помочь пережить трудности, справиться с навалившимися проблемами.
- Стилист, косметолог, диетолог. Умение следить за собой и чувствовать красоту развито у девушек значительно лучше, чем у мужчин, поэтому можно окончить курсы парикмахеров. Дамы бывают отличными стилистами, работниками салонов красоты, модельерами, дизайнерами интерьера.
пример
Рассмотрим совместное распределение вероятностей и приведено в таблице ниже.
Икс{\ displaystyle X}Y{\ displaystyle Y}
| п(Иксзнак равноИкс,Yзнак равноу){\ displaystyle \ operatorname {P} (X = x, Y = y)} | узнак равно-1{\ displaystyle y = -1} | узнак равно{\ displaystyle y = 0} | узнак равно1{\ displaystyle y = 1} |
| Иксзнак равно{\ displaystyle x = 0} | {\ displaystyle 0} | 13{\ displaystyle 1/3} | {\ displaystyle 0} |
| Иксзнак равно1{\ displaystyle x = 1} | 13{\ displaystyle 1/3} | {\ displaystyle 0} | 13{\ displaystyle 1/3} |
Для этого совместного распределения предельными распределениями являются:
- п(Иксзнак равноИкс)знак равно{13за Иксзнак равно23за Иксзнак равно1{\ displaystyle \ operatorname {P} (X = x) = {\ begin {cases} 1/3 & \ quad {\ text {for}} x = 0 \\ 2/3 & \ quad {\ text {for}} x = 1 \ end {case}}}
- п(Yзнак равноу)знак равно{13за узнак равно-113за узнак равно13за узнак равно1{\ displaystyle \ operatorname {P} (Y = y) = {\ begin {cases} 1/3 & \ quad {\ text {for}} y = -1 \\ 1/3 & \ quad {\ text {for}} y = 0 \\ 1/3 & \ quad {\ text {for}} y = 1 \ end {case}}}
Это дает следующие ожидания и отклонения:
- μИксзнак равно23{\ displaystyle \ mu _ {X} = 2/3}
- μYзнак равно{\ displaystyle \ mu _ {Y} = 0}
- σИкс2знак равно29{\ Displaystyle \ sigma _ {X} ^ {2} = 2/9}
- σY2знак равно23{\ Displaystyle \ sigma _ {Y} ^ {2} = 2/3}
Следовательно:
- ρИкс,Yзнак равно1σИксσYE(Икс-μИкс)(Y-μY)знак равно1σИксσY∑Икс,у(Икс-μИкс)(у-μY)п(Иксзнак равноИкс,Yзнак равноу)знак равно(1-23)(-1-)13+(-23)(-)13+(1-23)(1-)13знак равно{\ displaystyle {\ begin {align} \ rho _ {X, Y} & = {\ frac {1} {\ sigma _ {X} \ sigma _ {Y}}} \ operatorname {E} \\ & = {\ frac {1} {\ sigma _ {X} \ sigma _ {Y}}} \ sum _ {x , y} {(x- \ mu _ {X}) (y- \ mu _ {Y}) \ operatorname {P} (X = x, Y = y)} \\ & = (1-2 / 3) (- 1-0) {\ frac {1} {3}} + (0-2 / 3) (0-0) {\ frac {1} {3}} + (1-2 / 3) (1-0) {\ frac {1} {3}} = 0. \ end {выравнивается}}}
Расчет коэффициента корреляции
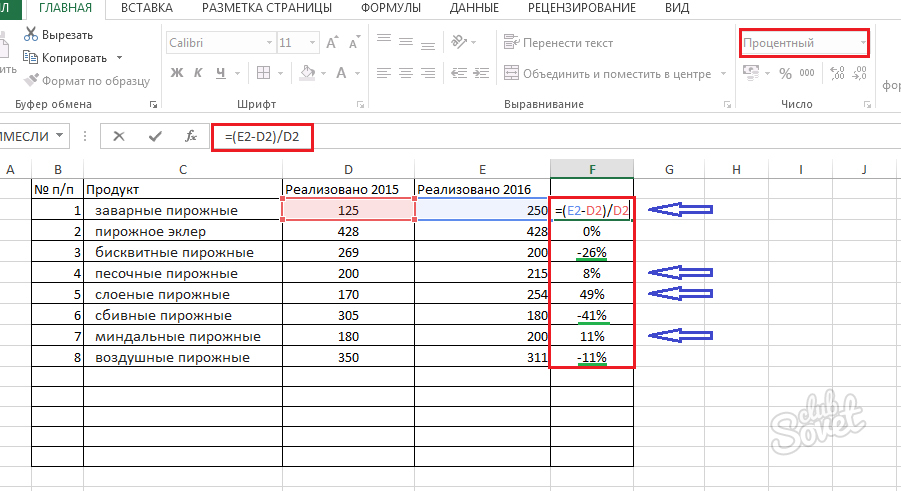
Теперь давайте попробуем посчитать коэффициент корреляции на конкретном примере. Имеем таблицу, в которой помесячно расписана в отдельных колонках затрата на рекламу и величина продаж. Нам предстоит выяснить степень зависимости количества продаж от суммы денежных средств, которая была потрачена на рекламу.
Способ 1: определение корреляции через Мастер функций
Одним из способов, с помощью которого можно провести корреляционный анализ, является использование функции КОРРЕЛ. Сама функция имеет общий вид КОРРЕЛ(массив1;массив2).
- Выделяем ячейку, в которой должен выводиться результат расчета. Кликаем по кнопке «Вставить функцию», которая размещается слева от строки формул.
В списке, который представлен в окне Мастера функций, ищем и выделяем функцию КОРРЕЛ. Жмем на кнопку «OK».
Открывается окно аргументов функции. В поле «Массив1» вводим координаты диапазона ячеек одного из значений, зависимость которого следует определить. В нашем случае это будут значения в колонке «Величина продаж». Для того, чтобы внести адрес массива в поле, просто выделяем все ячейки с данными в вышеуказанном столбце.
В поле «Массив2» нужно внести координаты второго столбца. У нас это затраты на рекламу. Точно так же, как и в предыдущем случае, заносим данные в поле.
Жмем на кнопку «OK».
Как видим, коэффициент корреляции в виде числа появляется в заранее выбранной нами ячейке. В данном случае он равен 0,97, что является очень высоким признаком зависимости одной величины от другой.
Способ 2: вычисление корреляции с помощью пакета анализа
Кроме того, корреляцию можно вычислить с помощью одного из инструментов, который представлен в пакете анализа. Но прежде нам нужно этот инструмент активировать.
- Переходим во вкладку «Файл».
В открывшемся окне перемещаемся в раздел «Параметры».
Далее переходим в пункт «Надстройки».
В нижней части следующего окна в разделе «Управление» переставляем переключатель в позицию «Надстройки Excel», если он находится в другом положении. Жмем на кнопку «OK».
В окне надстроек устанавливаем галочку около пункта «Пакет анализа». Жмем на кнопку «OK».
После этого пакет анализа активирован. Переходим во вкладку «Данные». Как видим, тут на ленте появляется новый блок инструментов – «Анализ». Жмем на кнопку «Анализ данных», которая расположена в нем.
Открывается список с различными вариантами анализа данных. Выбираем пункт «Корреляция». Кликаем по кнопке «OK».
Открывается окно с параметрами корреляционного анализа. В отличие от предыдущего способа, в поле «Входной интервал» мы вводим интервал не каждого столбца отдельно, а всех столбцов, которые участвуют в анализе. В нашем случае это данные в столбцах «Затраты на рекламу» и «Величина продаж».
Параметр «Группирование» оставляем без изменений – «По столбцам», так как у нас группы данных разбиты именно на два столбца. Если бы они были разбиты построчно, то тогда следовало бы переставить переключатель в позицию «По строкам».
В параметрах вывода по умолчанию установлен пункт «Новый рабочий лист», то есть, данные будут выводиться на другом листе. Можно изменить место, переставив переключатель. Это может быть текущий лист (тогда вы должны будете указать координаты ячеек вывода информации) или новая рабочая книга (файл).
Когда все настройки установлены, жмем на кнопку «OK».
Так как место вывода результатов анализа было оставлено по умолчанию, мы перемещаемся на новый лист. Как видим, тут указан коэффициент корреляции. Естественно, он тот же, что и при использовании первого способа – 0,97. Это объясняется тем, что оба варианта выполняют одни и те же вычисления, просто произвести их можно разными способами.
Как видим, приложение Эксель предлагает сразу два способа корреляционного анализа. Результат вычислений, если вы все сделаете правильно, будет полностью идентичным. Но, каждый пользователь может выбрать более удобный для него вариант осуществления расчета.
Опишите, что у вас не получилось.
Наши специалисты постараются ответить максимально быстро.
Имитация кирпича для внутренней отделки своими руками
Несколько важных замечаний
1. Коэффициент корреляции Пирсона чувствителен к выбросам. Одно аномальное значение может существенно исказить коэффициент. Поэтому перед проведением анализа следует проверить и при необходимости удалить выбросы. Другой вариант – перейти к ранговому коэффициенту корреляции Спирмена. Рассчитывается также, только не по исходным значениям, а по их рангам (пример показан в ролике под статьей).
2. Синоним корреляции – это взаимосвязь или совместная вариация. Поэтому наличие корреляции (r ≠ 0) еще не означает причинно-следственную связь между переменными. Вполне возможно, что совместная вариация обусловлена влиянием третьей переменной. Совместное изменение переменных без причинно-следственной связи называется ложная корреляция.
3. Отсутствие линейной корреляции (r = 0) не означает отсутствие взаимосвязи. Она может быть нелинейной. Частично эту проблему решает ранговая корреляция Спирмена, которая показывает совместный рост или снижение рангов, независимо от формы взаимосвязи.
В видео показан расчет коэффициента корреляции Пирсона с доверительными интервалами, ранговый коэффициент корреляции Спирмена.
9.1.2. Проверка статистических гипотез о связи переменных
Выборочный коэффициент корреляции оценивает подразумеваемую исследователем реальную связь между переменными. Как и в случае оценки среднего значения, нас интересуют два вопроса: (1) Насколько сильна связь между переменными; (2) Насколько надежна наша оценка. Сила связи между переменными по всей генеральной совокупности существует объективно. Если ее измерять корреляцией, то она будет выражаться числом от −1 до 1. Выборочная корреляция этих переменных будет колебаться вокруг истинного показателя силы связи. Трудность состоит в том, что, получив выборочную корреляцию, мы не можем знать, ни насколько она отклоняется от истинного значения, ни даже в какую сторону. В случае корреляции оценка обычно выражается в терминах значимости.
Проделаем небольшое упражнение.
Упражнение 9.1.2(1). Возьмите две симметричные монеты достоинством в один рубль и один евро. Проведите серию четырех подбрасываний пары монет и запишите результаты в виде \( (x_1, y_1),\dots,(x_4, y_4) \) , полагая
\( x_i=0 \), если рубль выпал цифрой;
\( x_i=1 \), если рубль выпал гербом;
\( y_i=0 \), если евро выпал цифрой;
\( y_i=1 \), если евро выпал гербом.
Подсчитайте коэффициент корреляции Пирсона. Истинная корреляция между результатами двух монет равна, разумеется, нулю. Повторите процедуру несколько раз и убедитесь, что нулевое значение выборочного коэффициента корреляции выпадает примерно один раз из трех. При многократном повторении опыта можно убедиться, что его результат имеет некоторое распределение, симметричное относительно нуля. Это распределение зависит от объема выборки n: чем больше n, тем меньше дисперсия распределения, тем ближе к нулю ее вероятные значения.
В таблице 9.1.2(2) приведены двухсторонние квантили распределения выборочного коэффициента корреляции по Пирсону для \( n=10 \). Они рассчитаны для выборок, полученных испытаниями двух нормально распределенных случайных величин, теоретическая корреляция между которыми равна нулю. Дихотомический результат подбрасывания монеты не распределен нормально, однако некоторое представление о возможных результатах наших испытаний табличный квантиль все же дает.
Таблица 9.1.2(2) Двусторонние квантили распределения коэффициента Пирсона для n = 10
| \( \alpha \) | 0.05 | 0.025 | 0.01 | 0.005 |
| \( r_\alpha(10) \) | 0.497 | 0.576 | 0.658 | 0.709 |
Обычно при исследовании связи переменных статистической гипотезой \( H_0 \) будет гипотеза об отсутствии связи, т.е. о независимости переменных. Альтернативная гипотеза \( H_1 \) (т.е. гипотеза, к которой мы склоняемся, получив большие по модулю значения выборочной корреляции) будет утверждать только наличие связи . Можно оценить значимость относительно данного результата (полученной парной выборки) гипотез о других значениях теоретической корреляции, но это требует некоторых дополнительных усилий (см. подпараграф ). Если истинна гипотеза \( H_0 \), то выборочный коэффициент корреляции будет принимать значения, более или менее близкие к нулю. Если выборочная корреляция принимает достаточно большое по модулю значение, которому соответствует значимость, измеряемая маленьким числом, то мы склоняемся к гипотезе \( H_1 \) о наличии связи, но без указания точного значения теоретической корреляции.
Можно заметить, что если верна гипотеза об отсутствии зависимости между случайными величинами, то выборочный коэффициент при \( n=10 \) может принимать тем не менее довольно большие значения, так что уровень значимости 0.05 для принятия гипотезы о зависимости случайных величин требует, чтобы выборочный коэффициент корреляции достигал почти 0.5 (см. ). В связи с этим надо иметь в виду, что даже выборочная корреляция, например 0.6, вполне может согласовываться с истинной корреляцией, равной 0.2 .
Корреляционные матрицы
Корреляционная матрица случайных величин — это матрица, элементом которой является . Если меры корреляции используется коэффициенты продукта момент, корреляционная матрица является таким же , как ковариационная матрица из стандартизованных случайных величин для . Это применимо как к матрице корреляций совокупности (в этом случае — стандартное отклонение совокупности), так и к матрице корреляций выборки (в этом случае означает стандартное отклонение выборки). Следовательно, каждая матрица обязательно является положительно-полуопределенной . Более того, корреляционная матрица является строго положительно определенной, если никакая переменная не может иметь все свои значения, точно сгенерированные как линейная функция значений других.
п{\ displaystyle n}Икс1,…,Иксп{\ Displaystyle X_ {1}, \ ldots, X_ {n}}п×п{\ Displaystyle п \ раз п}(я,j){\ displaystyle (я, j)}корр(Икся,Иксj){\ displaystyle \ operatorname {corr} (X_ {i}, X_ {j})} Иксяσ(Икся){\ Displaystyle X_ {i} / \ sigma (X_ {i})}язнак равно1,…,п{\ Displaystyle я = 1, \ точки, п}σ{\ displaystyle \ sigma}σ{\ displaystyle \ sigma}
Матрица корреляции является симметричной, поскольку корреляция между и такая же, как корреляция между и .
Икся{\ displaystyle X_ {i}}Иксj{\ displaystyle X_ {j}}Иксj{\ displaystyle X_ {j}}Икся{\ displaystyle X_ {i}}
Матрица корреляции появляется, например, в одной формуле для , меры согласия в множественной регрессии .
В статистическом моделировании матрицы корреляции, представляющие взаимосвязи между переменными, подразделяются на различные структуры корреляции, которые различаются такими факторами, как количество параметров, необходимых для их оценки. Например, в заменяемой корреляционной матрице все пары переменных моделируются как имеющие одинаковую корреляцию, поэтому все недиагональные элементы матрицы равны друг другу. С другой стороны, авторегрессионная матрица часто используется, когда переменные представляют собой временной ряд, поскольку корреляции, вероятно, будут больше, когда измерения ближе по времени. Другие примеры включают независимый, неструктурированный, M-зависимый и Toeplitz.
Литература
- Гмурман В. Е.<span title=»Статья «Гмурман, Владимир Ефимович» в русском разделе отсутствует»>ru</span>uk. Теория вероятностей и математическая статистика: Учебное пособие для вузов. — 10-е издание, стереотипное. — Москва: Высшая школа, 2004. — 479 с. — ISBN 5-06-004214-6.
- Елисеева И. И., Юзбашев М. М. Общая теория статистики: Учебник / Под ред. И. И. Елисеевой. — 4-е издание, переработанное и дополненное. — Москва: Финансы и Статистика, 2002. — 480 с. — ISBN 5-279-01956-9.
- Общая теория статистики: Учебник / Под ред. Р. А. Шмойловой. — 3-е издание, переработанное. — Москва: Финансы и Статистика, 2002. — 560 с. — ISBN 5-279-01951-8.
- Суслов В. И., Ибрагимов Н. М., Талышева Л. П., Цыплаков А. А. Эконометрия. — Новосибирск: СО РАН, 2005. — 744 с. — ISBN 5-7692-0755-8.
Открытие загрузочной флешки через BIOS
Мало только сделать загрузочный флеш-накопитель. Случается так, что система перестаёт работать. В таком случае образ, записанный на флешку, необходимо открыть через настройки BIOS. Независимо от времени выпуска BIOS, названия, находящиеся в нем, остаются практически неизменными.
После того как вы зашли в BIOS, необходимо открыть «Advanced BIOS Features», в которой размещены устройства, в порядке запуска. Например, сначала загружается жесткий диск, при его отказе система обращается к CDROM. Не найдя системы и на нем, она переходит к USB-HDD. Что нам и надо. Поставив на первое место USB-HDD, сохраняем настройки и выходим из BIOS. При перезагрузке появится меню установки ОС. На некоторых современных системных платах существует специальное Boot Menu, войти в которое можно при загрузке ПК, нажимая F8 или F12, в зависимости от фирмы-изготовителя «материнки», где очень просто можно выбрать загрузку ПК с записанного USB-накопителя. При загрузке ОС через BIOS может возникнуть несколько проблем, таких как:
- Системная плата не может поддерживать загрузку с внешнего устройства. Это возможно при таком случае, когда «материнка» была сделана до 2003 года;
- Обнаружение некорректной загрузочной флеш-карты. Вероятно, при записи операционной системы были допущены какие-либо ошибки. Проверьте загрузочную флешку на другом ПК;
- Отключение контроллера USB в BIOS.
Вычисление коэффициента посредством мастера функций
Предположим, что требуется установить связь между затратами на рекламу и объемом продаж какой-либо продукции. Для этого будем использовать коэффициент корреляции в Excel.
Порядок действий:
- Кликнуть по ячейке, в которой должен появиться результат.
- Нажать кнопку «Вставить формулу».
- В появившемся окне выбрать категорию «Полный алфавитный перечень».
- Найти и активировать функцию «КОРРЕЛ».
- Кликнуть «ОК».
- В открывшемся окне аргументов поставить курсор в поле «Массив 1», выделить первый столбец с данными.
- Поставить курсор в поле «Массив 2», выделить второй столбец из таблицы.
- Кликнуть «ОК».
В выделенной ячейке появляется результат вычислений корреляции в Excel.
Расчёт с помощью пакета анализа
Прежде чем воспользоваться инструментом корреляционного анализа, его нужно активировать. Для этого необходимо выполнить следующие действия:
- Выполнить действия «Файл» — «Сведения» — «Параметры».
- В появившемся окне перейти в раздел «Надстройки». В нижней части окна в выпадающем списке выбрать «Надстройки Excel». Нажать кнопку «Перейти».
- В открывшемся окне «Надстройки» следует о и нажать «ОК»
Чтобы воспользоваться пакетом, следует:
- На панели задач активировать вкладку «Данные».
- Нажать кнопку «Анализ данных».
- В новом окне выделить строку «Корреляция» и нажать «ОК». Появится окно с параметрами.
- Для выбора входного интервала необходимо установить курсор в соответствующее поле и выделить сразу оба столбца.
- Параметр группировки следует о. Вывод результатов возможен в указанное место, на новый лист или в новую книгу.
- Следует отметить соответствующее поле.
Работа со сводными таблицами в MS Excel
После указание всех параметров следует нажать «ОК».
Значение получилось тем же, что и в первом случае.
Поле корреляции (диаграмма рассеяния)
Корреляционное поле — это графическое отображение исходных данных. По расположению точек можно определить наличие зависимости и ее характер.
В редакторе Excel построение выполняется с помощью инструмента «Диаграмма»:
- Выделить столбцы с данными.
- Кликнуть «Вставка» — «Точечная» — «Точечная с маркерами».
- Результат построения корреляционной матрицы.
- По расположению точек на диаграмме можно сделать вывод о том, что прослеживается сильная положительная корреляционная зависимость между величиной затрат на маркетинг и объемом продаж.
- Для того, чтобы использовать диаграмму в практических целях, можно добавить линию тренда и уравнение. Для этого нужно выполнить следующие действия:
- Кликнуть правой кнопкой мыши на любой точке диаграммы.
- В контекстном меню выбрать «добавить линию тренда».
- Настроить параметры линии тренда (можно оставить по умолчанию).
- Нажать кнопку «закрыть».
Примеры использование корреляционного анализа
Как уже отмечалось выше, вычислить соотношение можно между любыми числовыми величинами. Обнаруженная высокая корреляция позволяет прогнозировать протекание каких-либо процессов в научных исследованиях, бизнесе, общественной жизни.
В рассмотренном выше примере была установлена высокая положительная корреляция между затратами на рекламу и объемом продаж определенного вида продукции. Кроме того, была определена формула, связывающая эти два показателя. Это исследование позволяет руководителю предприятия грамотно спланировать затраты на рекламу, с учетом необходимого размера продаж.
Другие примеры использования коэффициента корреляции:
Что делать, если лист или книга в Excel защищены паролем – как снять защиту
Редактор электронных таблиц Microsoft Excel является удобным инструментом для вычисления и наглядного представления результатов вычисления коэффициента корреляции.