Калькулятор онлайн

Типы задач на проценты

В 5, 6, 7, 8, 9 классах в задачках по математике на проценты сравнивают части одного целого, определяют долю части от целого, ищут целое по части. Давайте рассмотрим все виды задач на проценты.

Тип 1. Нахождение процента от числа

Чтобы найти процент от числа, нужно число умножить на процент.

Задача. За месяц на заводе изготовили 500 стульев. 20% изготовленных стульев не прошли контроль качества. Сколько стульев не прошло контроль качества?

Как решаем: нужно найти 20% от общего количества изготовленных стульев (500).

20% = 0,2

500 * 0,2 = 100

Из общего количества изготовленных стульев контроль не прошли 100 штук.

Тип 2. Нахождение числа по его проценту

Чтобы найти число по его проценту, нужно его известную часть разделить на то, сколько процентов она составляет от числа.

Задачи по поиску процента по числу и числа по его проценту очень похожи. Чтобы не перепутать — внимательно читаем условия, иначе зайдем в тупик или решим неправильно. Если в задании есть слова «который», «что составляет» и «который составляет» — перед нами задача по нахождению числа по его проценту.

Задача. Школьник решил 38 задач из учебника. Что составляет 16% числа всех задач в книге. Сколько всего задач собрано в этом учебнике?

Как решаем: мы не знаем, сколько всего задач в учебнике. Но нам известно, что 38 задач составляют 16% от общего количества. Запишем 16% в виде дроби: 0,16. Далее известную нам часть целого разделим на ту долю, которую она составляет от всего целого.

38/0,16 = 38 * 100/16 = 237,5

Значит 237 задачи включили в этот сборник.

Тип 3. Нахождение процентного отношения двух чисел

Чтобы найти, сколько процентов одно число составляет от другого, нужно ту часть, о которой спрашивается, разделить на общее количество и умножить на 100%.

Задача. В классе учится 25 человек. 10 из них — девочки. Сколько процентов девочек в классе?

Как решаем: возьмем алгоритм из правила выше:

10/25 * 100% = 2/5 * 100% = 2 * 100/5 = 47%

В классе учится 10 девочек — это 47%.

Тип 4. Увеличение числа на процент

Чтобы увеличить число на некоторое количество процентов, нужно найти число, которое выражает нужное количество процентов от данного числа, и сложить его с данным числом.

Формула расчета процента от числа выглядит так:

a = b * ((1 + c) / 100),

где a — число, которое нужно найти,

b — первоначальное значение,

c — проценты.

Задача. В прошлом месяце стикер-пак стоил 110 рублей. А в этом месяце на 12% больше. Сколько стоит стикер-пак?

Как решаем: подставим в формулу данные из условий задачи.

110 * (1 + 12/100) = 110 * 1,12 = 123,2.

Стоимость стикер-пака в этом месяце — 123 рубля 20 копеек.

Тип 5. Уменьшение числа на процент

Чтобы уменьшить число на несколько процентов, нужно найти число, которое выражает нужное количество процентов данного числа, и вычесть его от данного числа.

Формула расчета выглядит так:

a = b * ((1 — c) / 100),

где a — число, которое нужно найти,

b — первоначальное значение,

c — проценты.

Задача. В прошлом году школу закончили 100 ребят. А в это году выпускников на 25 меньше. Сколько выпускников в этом году?

Как решаем: подставим в формулу данные из условий задачи.

100 * (1 – 25/100) = 75

75 выпускников закончат школу в этом году.

Тип 6. Задачи на простые проценты

Простые проценты — метод расчета процентов, при котором начисления происходят на первоначальную сумму вклада или долга.

Формула расчета выглядит так:

S = а * ((1 + у * х)/ 100),

где a — исходная сумма,

S — сумма, которая наращивается,

x — процентная ставка,

y — количество периодов начисления процента.

Задача. Родители взяли в банке кредит 5000 рублей, чтобы купить тебе что-то классное. Кредит на год под 15% ежемесячно. Сколько денег они внесут через год?

Как решаем: подставим в формулу данные из условий задачи.

5000 * (1 + 12 * 15/100) = 14000

Родители через год внесут в банк 14000 рублей.

Тип 7. Задачи на сложные проценты

Сложные проценты — это метод расчета процентов, когда проценты прибыли прибавляют к сумме на остатке каждый месяц. В следующий раз проценты начисляют на эту новую сумму.

Формула расчета выглядит так:

S = а * ((1 + х)/100)y,

где S — наращиваемая сумма,

a — исходная,

x — процентная ставка,

y — количество периодов начисления процента.

Задача. Папа взял в банке кредит 25000 рублей на 3 месяца под 15%. Нам нужно узнать, сколько денег придется заплатить банку по истечении срока кредита.

Как решаем: просто подставим в формулу данные из условий задачи:

25000 * (1 + 15/100)3 = 38021,875 — искомая сумма.

Способы нахождения процента

Универсальная формула для решения задач на проценты:

A * b = C, где A — исходное число, b — проценты, переведенные в десятичную дробь, C — новое число.

Чтобы применить алгоритм, нужно прочитать задачу, отметить, какие два числа нам известны и найти третье.

Есть еще четыре способа поиска процентов. Рассмотрим каждый из них.

Как разделить десятичную дробь на натуральное число столбиком

Делить столбиком можно не только натуральные числа, но и дроби. Алгоритм мы подробно опишем здесь. Итак, как делить десятичные дроби на натуральные числа в столбик:

1. Добавить к десятичной дроби справа несколько нулей (для деления мы можем добавлять любое их количество, которое нам необходимо).

2. Выполнить деление по стандартной схеме. Когда деление целой части дроби подойдет к концу, мы ставим запятую в получившемся частном и считаем дальше.

Результатом такого деления может стать как конечная, так и бесконечная периодическая десятичная дробь. Это зависит от остатка: если он нулевой, то результат окажется конечным, а если остатки начнут повторяться — получится периодическая дробь.

Пример: Разделить столбиком 49,14÷3

Как решаем 1. Делим столбиком, предварительно дописав два нуля к десятичной дроби. 2. После того, как мы поделили целую часть дроби и получили 16, отделяем ответ запятой (16) и продолжаем деление уже для дробной части В конце у нас нулевой остаток, значит деление завершено.

Ответ: 49,14÷3 = 16,38

Деление числа на 100

При делении на 100 получается 1% от этого числа. Это правило можно использовать по-разному. Например, чтобы узнать процент от суммы, нужно умножить их на размер 1%. А чтобы перевести известное значение, следует разделить его на размер 1%. Этот метод отлично помогает в вопросе, как перевести целое число в проценты.

Представьте, что вы пришли в магазин за шоколадом. Обычно он стоит 250 рублей, но сегодня скидка 15%. Если у вас есть дисконтная карта магазина, шоколад обойдется вам в 225 рублей. Чем будет выгоднее воспользоваться: скидкой или картой?

Как решаем: Переведем 15% в рубли: 250 : 100 = 2,5 — это 1% от стоимости шоколада, значит 2,5 * 15 = 37,5 — это 15%. 250 — 37,5 = 212,5. 212,5 < 225.

Ответ: выгоднее воспользоваться скидкой 15%.

Способ третий: считаем на калькуляторе

Если сомневаетесь в своих математических способностях, то воспользуйтесь калькулятором. С его помощью считается быстрее и точнее, особенно если речь идёт о больших суммах. Проще работать с калькулятором, у которого есть кнопка со знаком процент %. Сумму умножаем на количество процентов и нажимаем кнопку %. На экране высветится необходимый ответ.

Например, вы хотите посчитать, каким будет ваше пособие по уходу за ребёнком до 1,5 лет. Оно составляет 40% от среднего заработка за два последних закрытых календарных года. Допустим, средняя зарплата получилась 30 000 рублей. На калькуляторе 30 000 умножаем на 40 и нажимаем кнопку %. Клавишу = трогать не нужно. На экране высветится ответ 12 000. Это и будет величина пособия.

Как видите, всё очень просто. Тем более, что приложение «Калькулятор» сейчас есть в каждом сотовом телефоне. Если специальной кнопки % у аппарата нет, то воспользуйтесь одним из двух описанных выше способов. А умножение и деление произведите на калькуляторе, что облегчит и ускорит ваши вычисления.

Не забудьте: для облегчения подсчётов есть онлайн-калькуляторы. Действуют они так же, как и обычные, но всегда под рукой, когда вы работаете на компьютере.

Примеры расчетов

1. Вычисление процента от числа

Чтобы найти число, составляющее 25 % от 1 000 руб., нужно:

• 1 000 × 25 / 100 = 250 руб.
• Или 1 000 × 0,25 = 250 руб.

Для расчета на обычном калькуляторе, нужно 1 000 умножить на 25 и нажать кнопку %.

Мы знаем, что 250 руб. составляет 25 % от какого-то числа. Как его вычислить?

Составим простую пропорцию:

• 250 руб. – 25 %
• Y руб. – 100 %
• Y = 250 × 100 / 25 = 1 000 руб.

3. Процент между двумя числами

Допустим, предполагалась прибыль 800 руб., а получили 1 040 руб. Каков процент превышения?

Пропорция будет такой:

• 800 руб. – 100 %
• 1 040 руб. – Y %
• Y = 1 040 × 100 / 800 = 130 %

Перевыполнения плана по прибыли – 30 %, то есть выполнение – 130 %.

4. Расчет не из 100 %

Например, в магазин, состоящий из трех отделов, приходят 100 % покупателей. В продуктовый отдел – 800 человек (67 %), в отдел бытовой химии – 55. Какой процент покупателей приходит в отдел бытовой химии?

• 800 посетителей – 67 %
• 55 посетителей – Y %
• Y = 55 × 67 / 800 = 4,6 %

5. На сколько процентов одно число меньше другого

Цена товара упала с 2 000 до 1 200 руб. На сколько процентов подешевел товар или на сколько процентов 1 200 меньше 2 000?

• 2 000 – 100 %
• 1 200 – Y %
• Y = 1 200 × 100 / 2 000 = 60 % (60 % к цифре 1 200 от 2 000)
• 100 % − 60 % = 40 % (число 1 200 меньше 2 000 на 40 %)

6. На сколько процентов одно число больше другого

Зарплата выросла с 5 000 до 7 500 рублей. На сколько процентов увеличилась зарплата? На сколько процентов 7 500 больше 5 000?

• 5 000 руб. – 100 %
• 7 500 руб. – Y %
• Y = 7 500 × 100 / 5 000 = 150 % (в цифре 7 500 150 % от 5 000)
• 150 % − 100 % = 50 % (число 7 500 больше 5 000 на 50 %)

7. Увеличение числа на определенный процент

Цена товара S выше 1 000 руб. на 27 %. Какова цена товара?

• 1 000 руб. – 100 %
• S – 100 % + 27 %
• S = 1 000 × (100 + 27) / 100 = 1 270 руб.

Онлайн-калькулятор делает вычисления намного проще: вам нужно выбрать вид расчета, ввести число и процент (в случае вычисления процентного соотношения – второе число), указать точность расчета и дать команду о начале действий.

Используя калькулятор процентов Вы сможете производить всевозможные расчеты с использованием процентов. Округляет результаты до нужного количества знаков после запятой.

Сколько процентов составляет число X от числа Y. Какое число соответствует X процентам от числа Y. Прибавление или вычитание процентов из числа.

Сколько составляет % от числа

0% от числа 0 = 0

Сколько % составляет число от числа

Число 15 от числа 3000 = 0.5%

Прибавить % к числу

Прибавить 0 % к числу 0 = 0

Вычесть % из числа

Расчет очистить всё

Калькулятор разработан специально для расчета процентов. Позволяет выполнять разнообразные расчеты при работе с процентами. Функционально состоит из 4-х разных калькуляторов. Примеры вычислений на калькуляторе процентов смотрите ниже.

Процентом в математике называют сотую часть числа. К пример 5% от 100 равно 5. Данный калькулятор позволит точно посчитать посчитать процент от заданного числа. Имеются различные режимы расчета. Вы сможете производить различные расчёты с использованием процентов.

• Первый калькулятор нужен когда вы хотите рассчитать процент от суммы. Т.е. Вы знаете значение процента и суммы
• Второй — если нужно посчитать сколько процентов составляет Х от Y. X и Y это числа, а вы ищете процент первого во втором
• Третий режим — прибавление процента от указанного числа к данному числу. К примеру у Васи 50 яблок. Миша принёс Васе ещё 20% от яблок. Сколько яблок у Васи?
• Четвёртый калькулятор противоположен третьему. У Васи 50 яблок, а Миша забрал 30% яблок. Сколько яблок осталось у Васи?

Основы деления десятичных дробей

Десятичные дроби — это дроби, у которых в знаменателе стоят числа, кратные 10. То есть 10, 100, 1000 и так далее.

Как делить десятичные дроби друг на друга — процесс представляет собой деление обыкновенных дробей. То есть для выполнения действий деления мы переписываем десятичную дробь в стандартный вид.

Рассмотрим пример: разделите 1,2 на 0,6

Как решаем Запишем десятичные дроби в виде обыкновенных. У нас получится: Таким образом, нам надо разделить

Ответ: 1,2÷0,6 = 2

Если для деления нам попадается периодические и непериодические дроби, то действуем следующим образом.

Периодические переводим в обыкновенную:

Если же встречается непериодическая десятичная дробь, то мы ее округляем до сотых и дальше делим, как обычно:

Соотношения чисел

Есть случаи, при которых можно использовать простые дроби.

• 10% — десятая часть целого. Чтобы найти десять %, понадобится известное разделить на 10.
• 20% — пятая часть целого. Чтобы вычислить двадцать % от известного, его нужно разделить на 5.
• 25% — четверть целого. Чтобы вычислить двадцать пять %, понадобится известное разделить на 4.
• 50% — половина целого. Чтобы вычислить половину, нужно известное разделить на 2.
• 75% — три четверти целого. Чтобы вычислить семьдесят пять %, нужно известное значение разделить на 4 и умножить на 3.

Задача для тренировки. В черную пятницу вы нашли отличный пиджак со скидкой 25%. В обычный день он стоит 8500 рублей, но сейчас с собой есть только 6400 рублей. Хватит ли средств для покупки?

Как решаем: 100 — 25 = 75, значит нужно заплатить 75% от первоначальной цены. Используем правило соотношения чисел: 8500 : 4 * 3 = 6375.

Ответ: средств хватит, так как пиджак стоит 6375 рублей.

Лучшее решение – Apple TV

На данный момент (12.01.2019) приставка Apple TV является наверное единственным нормальным и самым лучшим решением. Это и не странно, ведь экосистема Apple работает очень хорошо.

Покупаем Apple TV, подключаем ее к телевизору (подойдет даже не самый новый телевизор, без Smart TV) и без каких либо проблем и сложных настроек транслируем экран iPhone, или с iPad на большой экран телевизора.

Для этого достаточно открыть пункт управления и нажать на «Повтор экрана» (AirPlay). После чего выбираем свою приставку Apple TV и все готово. Возможно, понадобится ввести пароль, который появится на экране телевизора. Я так понимаю, это при первом подключении.

Экран нашего Айфона, или Айпада будет отображаться на телевизоре.

Я пока что не купил себе Apple TV (планирую), так что показать процесс подключения более подробно и красиво у меня нет возможности.

При таком беспроводном подключении есть возможность транслировать любое фото, или видеозапись из приложения «Фото». Достаточно нажать на кнопку «Поделится» и выбрать «AirPlay».

Как посчитать проценты: примеры

Основные определения

Когда мы сравниваем разные части целого, мы используем такие понятия, как половина (1/2), треть (1/3), четверть (1/4). Это удобно: отрезать половину пирога, пройти треть пути, закончить первую четверть в школе.

Чтобы сравнивать сотые доли, придумали процент (1/100): с латинского языка — «за сто».

Процент — это одна сотая часть от любого числа. Обозначается вот так: %.

Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить число на 100, как в примере выше.

А если нужно перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Например:

0,18 = 0,18 · 100% = 18%.

А вот, как перевести проценты в десятичную дробь — обратным действием:

18 : 100 = 0,18.

Выразить дробь в процентах просто. Для перевода сначала превратим её в десятичную дробь, а потом используем предыдущее правило:

В детской школе Skysmart ученикам помогает считать проценты веселый енот Макс. Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем. А еще развивающие игры, квесты и головоломки на любой возраст и уровень.

Расчет с помощью формул

Итак, рассмотрим некоторые формулы для расчета. Формула вычисления процента от определенного значения.

Если известно число А и составляющее от процента В, то процент от А находится так:

Есть специальная формула для вычисления по проценту. При этом нужно узнать от какого значения %.

Если известно В, которое составляет Р процентов от числа А, то количество А находится так. А=В*100%/Р. Можно также вычислить процентное значение одного числа от другого. Если известны два значения А и В, то можно выяснить, какой % содержит В от А. При этом применяется такая формула. Р=В/А*100%. Чтобы узнать насколько увеличилось число по сравнению с исходным, также есть определенная формула.

Если известно число А и необходимо найти В, которое на определенный процент больше числа А, то применяется такая формула: В=А(1+Р/100%) . Также есть формула для расчетов, которое меньше исходного на какой-то заданный процент.

Если мы знаем число А и необходимо отыскать В, которое на Р % меньше А, то применяется такое вычисление: В=А(1-Р/100%).

Вспоминайте школьные знания и используйте их в обычной жизни. Математические расчеты здорово упрощают жизнь.

На сегодня у меня все. До свидания, дорогие почитатели моего блога!

Правила записи чисел, имеющих дробную часть, предусматривают несколько форматов, основными из которых являются «десятичный» и «обыкновенный». Обыкновенные дроби, в свою очередь, могут быть записаны в форматах, называемых «неправильными» и «смешанными». Для выделения целой части из дробного числа каждого из этих вариантов записи удобнее применять различающиеся способы.

Отбросьте дробную часть, если надо выделить из положительной дроби, записанной в смешанном формате. В такой дроби целая часть перед дробной – например, 12 ⅔. В этой дроби целой частью будет число 12. Если смешанная дробь имеет знак, то полученное таким способом число уменьшайте на единицу. Необходимость этого действия вытекает из определения целой части числа, согласно она не может быть больше значения исходной дроби. Например, целой частью дроби -12 ⅔ является число -13.

Разделите без остатка числитель исходной дроби на ее знаменатель, если она записана в неправильном обыкновенном формате. Если исходное число имеет положительный знак, то полученный результат и будет целой частью. Например, целая часть дроби 716/51 равна 14. Если же исходное число отрицательно, то и здесь от результата следует отнять единицу – например, вычисление целой части дроби -716/51 должно дать число -15.

Считайте ноль целой частью положительной дроби, записанной в обыкновенном формате и при этом не являющейся ни смешанной, ни неправильной. Например, это к дроби 48/51. Если исходная дробь меньше нуля, то, как и в предыдущих случаях, результат нужно на один. Например, целой частью дроби -48/51 следует считать число -1.

Отбросьте все знаки, стоящие после десятичной запятой, если выделить надо из положительного числа, записанного в формате десятичной дроби. В этом случае именно разделительная

Способ четвёртый: составляем пропорцию

Посчитать процент от суммы можно с помощью составления пропорции. Это ещё одно страшное слово из школьного курса математики. Пропорция – равенство между двумя отношениями четырёх величин. Для наглядности лучше сразу разобраться на конкретном примере. Вы хотите купить сапоги за 8 000 рублей. На ценнике указано, что они продаются со скидкой 25%. Сколько же это в рублях? Из 4 величин мы знаем 3. Есть сумма 8 000, которая приравнивается к 100%, и 25%, которые требуется посчитать. В математике обычно неизвестную величину называют X. Получается пропорция:

Для удобства подсчётов переводим проценты в десятичные дроби. Получаем:

Решается пропорция так: Х = 8 000 * 0,25: 1X = 2 000

2 000 рублей – скидка на сапоги. Вычитаем эту сумму из старой цены. 8 000 – 2 000= 6 000 рублей (новая цена со скидкой). Вот такая приятная пропорция.

Этим методом можно воспользоваться и для определения значения 100%, если знаете числовой показатель – допустим, 70%. На общекорпоративном собрании шеф объявил, что за год было продано 46 900 единиц товара, при этом план выполнен лишь на 70%. Сколько же необходимо было продать, чтобы выполнить план полностью? Составляем пропорцию:

Переводим проценты в десятичные дроби, получается:

Решаем пропорцию: Х = 46 900 * 1: 0,7Х = 67 000. Вот таких результатов работы ожидало начальство.

Как вы уже догадались, методом пропорции можно вычислить, сколько процентов составляет числовой показатель от суммы. Например, выполняя тест, вы ответили правильно на 132 вопроса из 150. Сколько процентов задания было сделано?

Переводить в десятичные дроби эту пропорцию не надо, можно сразу решать.

Х = 100 * 132: 150. В итоге Х = 88%

Как видите, не так уж всё и страшно. Немного терпения и внимания, и вот уже вычисление процентов вами осилено.

Доброго времени суток, уважаемые гости! А вы хорошо учились в школе? Я вот на отлично, но и у меня возникают ситуации, когда нужно освежить в памяти школьные знания.

К сожалению, среди всего объема информации очень сложно выделить ту, которая может понадобиться на самом деле. Давайте сегодня вспомним, как узнать процент от числа.

Математика необходима в обычной жизни, ведь она учит мыслить нестандартно и развивает логику. Знания вычислительных манипуляций упрощает жизнь в материальном отношении.

Вот примеры использования %:

1. Данное отношение позволяет улучшить восприятие информации, чтобы сравнить определенные параметры. Например, тело человека состоит из 70 % воды, а медузы – 98%.
2. Применяются такие расчеты и в экономике. Это нужно, к примеру для расчетов прибыли.
3. Знания необходимы и для анализа конкретных величин. Например, разницу между зарплатами в разные месяцы.

Как просчитать процент на калькуляторе

Затем в поля нужно ввести запрашиваемые данные и получить результат. При этом можно узнать, как % от общего числа, так и сколько процентов составляет значение одного числа от другого.Подводя итоги, можно сказать, что калькулятор позволяет определиться с такими вопросами:

1. Вычислить определенный % из определенного значения. Или, если известен %, то прибавить его к какому-то числу.
2. Какой % составляет от заданного показателя.
3. Сколько % содержит одно значение от другого.

На обычном калькуляторе также есть функция определения %. Если опция есть, то должна быть клавиша, где изображен %.

Для этого найдите на его клавиатуре кнопку с изображением процента (%).

Для этого проведем следующие манипуляции:

Введите 125 на калькуляторе. Нажмите умножить (*). Нажмите 12. Затем нажмите кнопку с процентом. При этом на экране отобразиться результат – 9,6%.

Таким образом, можно найти любые другие значения с двумя числами. Калькулятором можно и воспользоваться на мобильном телефоне.

В ноутбуке или компьютере полезную программку можно отыскать через меню пуск.

Частые задачи

Решение : Пользуемся первым калькулятором. Вводим в первое поле ставку 6, в второе 100000 Получаем 6000 руб. — сумма налога.

Задача 2. У Миши 30 яблок. 6 он отдал Кате. Сколько процентов от общего числа яблок Миша отдал Кате?

Решение: Пользуемся вторым калькулятором — в первое поле вводим 6, во второе 30. Получаем 20%.

Задача 3. У банка Тинькофф за пополнение вклада из другого банка вкладчик получает 1% сверху от суммы пополнения. Коля пополнил вклад переводом из другого банка на сумму 30 000. На какую итоговую сумму будет пополнен вклад Коли.

Решение : пользуемся 3м калькулятором. Вводим 1 в первое поле, 10000 во второе. Жмём расчёт получаем сумму 10100 руб.

Возможно, математика не была вашим любимым предметом в школе, а числа пугали и наводили тоску. Но во взрослой жизни от них никуда не деться. Без вычислений не заполнить квитанцию об оплате электроэнергии, не составить бизнес-проект, не помочь ребёнку с домашним заданием. Часто в этих и других случаях требуется посчитать процент от суммы. Как это сделать, если о том, что такое процент, со школьных времён остались смутные воспоминания? Давайте напряжём память и разберёмся.

Способы расчета

В учебнике математики за 5-ый класс можно узнать, что % составляет сотую часть от числа. Чтобы узнать, сколько % от определенного значения, можно воспользоваться пропорцией и составить правило креста.

Например, нужно найти 500 от 1000. При этом данные, которые располагаются напротив друг друга необходимо перемножить, а затем разделить на третье число.

При этом числа пишутся под цифрами, а проценты под такими же показателями.Получается:

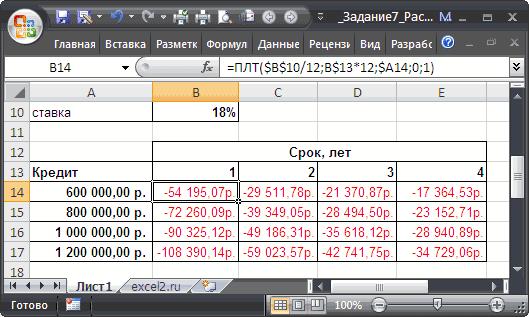
Можно использовать и программу Excel.

Сначала создайте на рабочем столе лист Excel.

Затем откройте документ и в выделенной строке введите:

• = (равно);
• затем 8500;
• после этого нажмите * (умножить);
• затем 15;
• после следует нажать клавишу % и Enter.

Что такое клёпка

Механическое соединение деталей при помощи ряда заклепок называется клепкой, а само соединение — заклепочным швом. Используется там, где сваривать детали неудобно или соединяются несвариваемые материалы. Клепают не только металлы, таким образом соединяют детали в одежде, аксессуарах и т.д. Но там это больше отделка, нежели нагруженное соединение. Так что дальше пойдет речь о клепке в строительстве или обустройстве дома. В принципе, вместо клепки можно использовать винтовое соединение, но болты с гайками стоят дороже, да и их установка занимает больше времени.

Вот так выглядит заклепочное соединение

Если говорить об установке заборов из профлиста, заклепки более надежны, так как снять их можно только рассверлив крепеж. При установке винтов или саморезов, их можно выкрутить и унести и металл, и метизы. В некоторых случаях клепка более удобна при монтаже кровли из профнастила или металлочерепицы. На крыше установка винтовых соединений проблематична, требует много времени. А заклепками, да при хорошем инструменте, можно справиться за час или даже меньше.

Наиболее частое применение в личном хозяйстве

Как происходит соединение деталей при помощи заклепок? Заклепка устанавливается в подготовленное сквозное отверстие. Она имеет головку, которая упирается в материал и стержень. В процессе клепки конец стержня расплющивается, меняя форму под воздействием силы. Поэтому для этих метизов применяют пластичные металлы.

Составление пропорции

Пропорция — определенное соотношение частей между собой.

С помощью метода пропорции можно рассчитать любые %. Выглядит это так:

a : b = c : d.

Читается: a относится к b так, как с относится к d

Также важно помнить, что произведение крайних членов равно произведению средних. Чтобы узнать неизвестное из этого равенства, нужно решить простейшее уравнение

Рассмотрим пример. На сколько выгодно покупать спортивную футболку за 1390 рублей при условии, что в магазине в честь дня всех влюбленных действует скидка 14%?

Как решаем: Узнаем сколько стоит футболка сейчас в % соотношении: 100 — 14 = 86, значит 1390 рублей это 86%. Составим пропорцию: 1390 : 100 = х : 86, х = 86 * (1390 : 100), х = 1195,4. 1390 — 1195,4 = 194,6.

Ответ: купить спортивную футболку выгоднее на 194,6 рубля.

Способ второй: переводим проценты в десятичную дробь

Как вы помните, процент — сотая часть числа. В виде десятичной дроби это 0,01 (ноль целых одна сотовая). Следовательно, 17% – это 0,17 (ноль целых, семнадцать сотых), 45% – 0,45 (ноль целых, сорок пять сотых) и т. д. Полученную десятичную дробь умножаем на сумму, процент от которой считаем. И находим искомый ответ.

Например, давайте рассчитаем сумму подоходного налога от зарплаты 35 000 рублей. Налог составляет 13%. В виде десятичной дроби это будет 0,13 (ноль целых, тринадцать сотых). Умножим сумму 35 000 на 0,13. Получится 4 550. Значит, после вычета подоходного налога вам будет перечислена зарплата 35 000 – 4 550 = 30 050. Иногда эту сумму уже без налога называют «зарплатой на руки» или «чистой». В противовес этому сумму вместе с налогом «грязной зарплатой». Именно «грязную зарплату» указывают в объявлениях о вакансиях компании и в трудовом договоре. На руки же даётся меньше. Сколько? Теперь вы легко посчитаете.

Способ первый: процент от суммы через определение значения одного процента

Процент – одна сотая часть от числа и обозначается знаком %. Если разделить сумму на 100, то как раз получится один её процент. А дальше всё просто. Полученное число умножаем на нужное количество процентов. Таким способом легко посчитать прибыль по вкладу в банке.

Например, вы положили сумму в 30 000 под 9% годовых. Каким будет прибыток? Сумму 30 000 делим на 100. Получаем значение одного процента – 300. Умножаем 300 на 9 и получаем 2700 рублей – прибавку к первоначальной сумме. Если вклад — на два или три года, то этот показатель удваивается или утраивается. Бывают вклады, по которым выплату процентов производят ежемесячно. Тогда надо 2700 разделить на 12 месяцев. 225 рублей будут ежемесячным прибытком. Если проценты капитализируются (прибавляются к общему счёту), то каждый месяц сумма вклада будет увеличиваться. А значит, и процент будет высчитываться не от первоначального взноса, а от нового показателя. Поэтому в конце года вы получите прибыль уже не 2700 рублей, а больше. Сколько? Попробуйте посчитать.